Um objeto cujo peso é 100 lbf (444,8 N) experimenta um decréscimo na energia cinética de 500 ftlbf(667,9 Nm) e um aumento na energia potencial de 1500 ftlbf (2033,7 Nm). A velocidade inicial e a altura do objeto, ambas em relação a superfície da Terra são 40 ft/s (12,2 m/s) e 30 ft (9,1 m), respectivamente. Considerando que g = 32,2 ft/s² (9,8 m/s²), determine
- a velocidade final, em ft/s
- a altura final, em ft
Passo 1
Vamos resolver mais pessoal. A figura que vocês veem abaixo é um esquema com os dados que a questão oferece. O objeto tem um decréscimo de energia cinética e um aumento na energia potencial, o que faz a gente ter uma noção que a velocidade final será menor e a altura final será maior
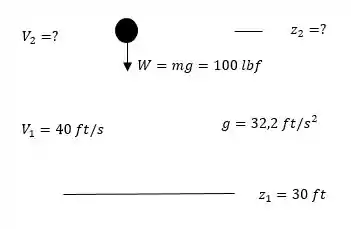
A variação de energia cinética e potencial, relembrando, é calculada por essas duas fórmulas aqui
Passo 2
Antes de calcularmos a variação de energia cinética, vamos achar o valor da massa do objeto.
A gente sabe que e assim
Com isso, a massa do objeto é
Agora, vamos substituir os valores na fórmula da variação de energia cinética
Passo 3
Para a gente achar a altura final, vamos pegar a fórmula da variação de energia potencial e substituir os valores que já sabemos
Como temos