Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 69
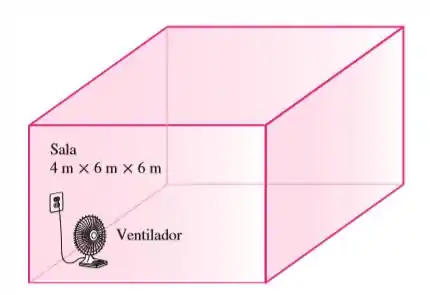
O quarto de uma estudante possui dimensões de . Ela liga um ventilador de antes de deixar o quarto em um dia de verão, esperando que o mesmo esteja mais fresco quando ela voltar à noite. Considerando que todas as portas e janelas estejam bem fechadas e descartando qualquer transferência de calor pelas paredes e janelas, determine a temperatura da sala quando a estudante voltar horas mais tarde. Use valores de calor específico à temperatura ambiente e considere que a sala está a e quando a estudante sai de manhã.
Passo 1
Hey hey, vamo lá! Uma estudante que vive num quarto liga o seu ventilador de pela manhã. A temperatura no quarto quando ela volta mais tarde deve ser determinada. Nós tomamos a sala como o sistema. O equilíbrio de energia pode ser expressado abaixo, certo? Portanto,
Logo, da formula da variação de energia:
Passo 2
Agora vamos achar a massa do ar. Temos que o volume da sala é:
Portanto, a massa de ar da sala é:
Passo 3
Tamo quase lá gente! O trabalho elétrico realizado pelo ventilador é de:
Substituindo e usando o valor na temperatura da sala: