Reconsidere o Prob. 4-140. Usando o EES (ou outro programa), estude os efeitos da temperatura inicial do gelo sobre a massa final necessária. Varie a temperatura do gelo entre -26 °C e 0 °C. Trace um gráfico para a massa do gelo em função de sua temperatura inicial e discuta os resultados.
Passo 1
A solução pelo o EES é:
"Conhecidos"rho_agua = 1 [kg/L]V = 0.3 [L]T_1_gelo = 0 [C]T_1 = 20 [C]T_2 = 5 [C]C_gelo = 2.11 [kJ/kg-C]C_água = 4.18 [kJ/kg-C]h_fusao = 333.7 [kJ/kg]T_1_aguafria = 0 [C]
m_agua = rho_agua*V "[kg]" "Massa da água""Balanço de energia"E_entra - E_sai = DELTAE_sist "[kJ]"E_entra = 0 "[kJ]"E_sai = 0"[kJ]"DELTAE_sist = DELTAU_agua+DELTAU_gelo"[kJ]"DELTAU_agua = m_agua*C_agua*(T_2 - T_1)"[kJ]"DELTAU_gelo = DELTAU_gelosolido+DELTAU_geloderretido"[kJ]"DELTAU_ gelosolido =m_gelo*C_gelo*(0-T_1_gelo) + m_gelo*h_fusao"[kJ]"DELTAU_ geloderretido =m_gelo*C_agua*(T_2 - 0)"[kJ]"m_gelo_gramas=m_gelo*convert(kg,g)"[g]"
"Resfriando com água fria:"DELTAE_sist = DELTAU_agua+DELTAU_aguafria"[kJ]"DELTAU_agua = m_agua*C_agua*(T_2_aguafria - T_1)"[kJ]"DELTAU_aguafria = m_aguafria*C_agua*(T_2_aguafria - T_1_aguafria)"[kJ]"m_aguafria_gramas=m_aguafria*convert(kg,g)"[g]
Passo 2
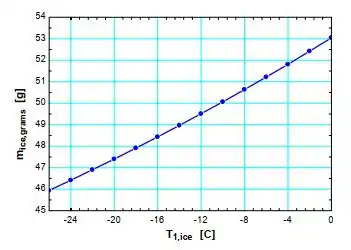
Resposta
Ei, a resposta está no passo a passo :)