Reconsidere o Prob. 4-77. Usando o EES (ou outro programa), mostre o processo descrito no problema em um diagrama P-v e investigue o efeito do expoente politópico n no trabalho de fronteira e na transferência de calor. Varie o expoente politrópico entre 1,1 e 1,6. Trace um gráfico do trabalho de fronteira e da transferência de calor em função do expoente politrópico e discuta os resultados.
Passo 1
O código em EES fica:
Procedure Work(P[2],V[2],P[1],V[1],n:W_in)If n=1 thenW_in=-P[1]*V[1]*ln(V[2]/V[1])ElseW_in=-(P[2]*V[2]-P[1]*V[1])/(1-n)endifEnd"Input Data"Vratio=0.5 "V[2]/V[1] = Vratio""n=1.3" "Polytropic exponent"P[1] = 100 [kPa]T[1] = (17+273) [K]m=1.5 [kg]MM=molarmass(nitrogen)R_u=8.314 [kJ/kmol-K]R=R_u/MMV[1]=m*R*T[1]/P[1]"Process equations"V[2]=Vratio*V[1]P[2]*V[2]/T[2]=P[1]*V[1]/T[1]"The combined ideal gas law forstates 1 and 2 plus the polytropic process relation give P[2] and T[2]"P[2]*V[2]^n=P[1]*V[1]^n"Conservation of Energy for the closed system:""E_in - E_out = DeltaE, we neglect Delta KE and Delta PE for the system, the nitrogen."Q_out= W_in-m*(u[2]-u[1])u[1]=intenergy(N2, T=T[1]) "internal energy for nitrogen as an ideal gas, kJ/kg"u[2]=intenergy(N2, T=T[2])Call Work(P[2],V[2],P[1],V[1],n:W_in)"The following is required for the P-v plots"{P_plot*spv_plot/T_plot=P[1]*V[1]/m/T[1]"The combined ideal gas law for states 1 and 2 plus the polytropic process relation give P[2] and T[2]"P_plot*spv_plot^n=P[1]*(V[1]/m)^n}{spV_plot=R*T_plot/P_plot"[m^3]"}
Passo 2
Variando o expoente politrópico, o diagrama P-v comparativo fica como mostrado na figura abaixo.
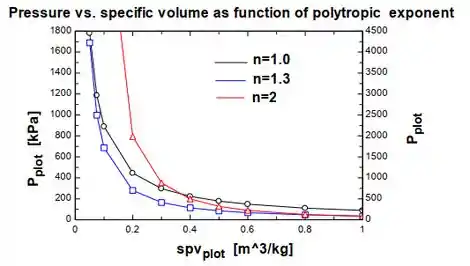
Passo 3
Gráficos para o trabalho de fronteira e o calor transferido para o sistema
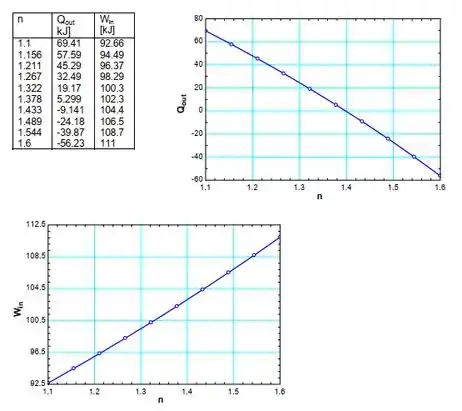
Resposta
Ei, a resposta está no passo a passo :)