Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 6.Problemas - Ex. 137
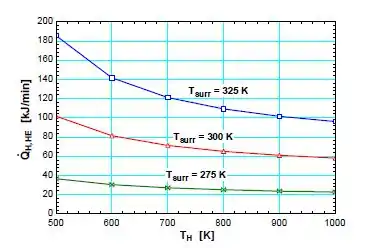
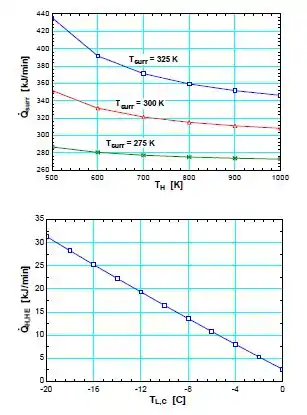
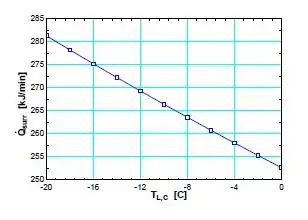
Reconsidere o Prob. 6–136. Utilizando o EES (ou outro programa), investigue os efeitos da temperatura da fonte da máquina térmica, da temperatura ambiente e da temperatura do espaço refrigerado sobre o fornecimento de calor necessário a máquina térmica e sobre a taxa total de rejeição de calor no ambiente. Varie a temperatura de fonte de 500 K a 1.000 K, a temperatura ambiente de 275 K a 325 K e a temperatura do espaço refrigerado de -20 °C a 0 °C. Trace um gráfico do fornecimento de calor necessário em função da temperatura da fonte considerando uma temperatura do espaço refrigerado correspondente a -15 °C e também as temperaturas ambientes de 275 K, 300 K e 325 K. Discuta os resultados.
Passo 1
Vamos lá! O programa utilizado é o EES como indicado pela questão, portanto os resultados são tabulados no passo 2 e plotados no passo 3.
Passo 2
Q_dot_L_R = 250 [kJ/min]
T_surr = 300 [K]
T_H = 900 [K]
T_L_C = -15 [C]
T_L =T_L_C+ 273
" Coeficiente de desempenho da geladeira Carnot:"
T_H_R = T_surr
COP_R = 1/(T_H_R/T_L-1)
" Entrada de energia para a geladeira:"
W_dot_in_R = Q_dot_L_R/COP_R
" A potência de saída do motor térmico deve ser:"
W_dot_out_HE = W_dot_in_R
" A eficiência do motor térmico é:"
T_L_HE = T_surr
eta_HE = 1 - T_L_HE/T_H
" A taxa de entrada de calor para o motor térmico é:"
Q_dot_H_HE = W_dot_out_HE/eta_HE
" Primeira lei aplicada ao motor térmico e à geladeira:"
Q_dot_L_HE = Q_dot_H_HE - W_dot_out_HE
Q_dot_H_R = Q_dot_L_R + W_dot_in_R
Portanto, a tabela com os valores é:
Passo 3
Logo, o gráfico resultante a partir dos valores tabelados é
Resposta
Ei, a resposta está no passo a passo :)