Refrigerante 134a é o fluido de trabalho de um sistema de bomba de calor por compressão de vapor que fornece 35 kW para aquecer uma residência em um dia em que a temperatura externa é inferior à temperatura de congelamento. Vapor saturado entra no compressor a 1,6 bar e líquido saturado sai do condensador, que opera a 8 bar. Determine para uma compressão isentrópica
(a) a vazão mássica do refrigerante, em kg/s.
(b) a potência do compressor, em kW.
(c) o coeficiente de desempenho.
Recalcule as grandezas dos itens (b) e (c) para uma eficiência isentrópica do compressor de 75%.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
O diagrama é mostrado abaixo
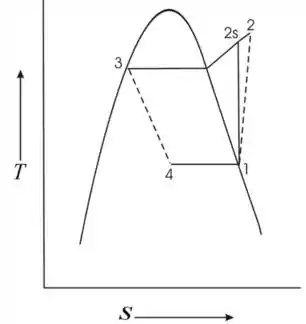
Passo 3
Obtendo as propriedades do refrigerante a pressão das tabelas de R-134a saturado
A entropia permanece constante no processo 1-2s:
Obtendo a entalpia no estado 2s da tabela de R-134a superaquecido a
Passo 4
A entalpia no estado 3 é igual a do líquido saturado. Pegando a entalpia da tabale de R-134a saturado a pressão de
Já que o processo 3-4 é um processo de estrangulamento, a entalpia permanece constante
Passo 5
a) calculando a taxa de vazão mássica do refrigerante no caso de compressão isentrópica
Passo 6
b) calculando a potência do compressor
Passo 7
c) calculando o coeficiente de performance
Passo 8
Refazendo as letras b) e c). Podemos achar a entalpia no estado 2 usando a compressão isentrópica,
Achamos a taxa de vazão mássica
Passo 9
b) a potência do compressor para a eficiência isentrópica
Passo 10
c) calculando o coeficiente de performance
Resposta
a)
b)
c)
b’)
c’)