Um sistema de bomba de calor por compressão de vapor usa Refrigerante 134a como fluido de trabalho e tem uma capacidade de aquecimento de 60.000 Btu/h (17,6 kW). O condensador opera a 200 lbf/in2 (1379 kPa) e a temperatura no evaporador é 0°F (–17,8°C). Na saída do evaporador o refrigerante se encontra no estado de vapor saturado e, na saída do condensador, no estado de líquido a 110°F (43,3°C). As quedas de pressão ao longo do evaporador e do condensador são desprezíveis. O processo de compressão é adiabático e a temperatura na saída do compressor é de 180°F (82,2°C). Determine
(a) a vazão mássica do refrigerante, em lb/min.
(b) a potência de acionamento do compressor, em HP.
(c) a eficiência isentrópica do compressor.
(d) o coeficiente de desempenho.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
É dado que:
- Capacidade de calor da bomba de calor:
- Pressão do condensador:
- Temperatura do evaporador:
- Temperatura de saída de condensador:
- Temperatura de saída do compressor:
O diagrama é mostrado abaixo
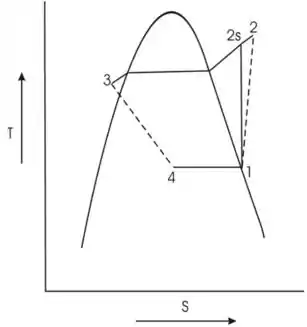
Passo 3
Das tabelas de R-134a saturado a
Das tabelas de R-134a superaquecido a e
Das tabelas de R-134a superaquecido a e
Passo 4
Das tabelas de R-134a saturado a
Dado que , o estado 3 está em sub resfriado
Das tabelas de R-134a saturado a
O processo 3-4 é de estrangulamento, então
Passo 5
a) a vazão mássica do refrigerante é
Passo 6
b) a potência de entrada no compressor é
Passo 7
c) a eficiência do compressor isentrópico
Passo 8
d) o coeficiente de performance é dado por
Resposta
a)
b)
c)
d)