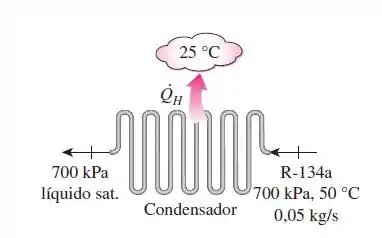
Refrigerante-134a e condensado em um sistema de refrigeração, rejeitando calor para o ar ambiente a . O refrigerante entra no condensador a e a uma taxa de , saindo como liquido saturado com a mesma pressão anterior. Determine a taxa de calor rejeitado no condensador, o COP desse ciclo de refrigeração, considerando que a carga de resfriamento a essas condições e de , e a taxa de destruição de exergia no condensador.

Um refrigerante esta sendo refrigerado e temos que determinar a taxa de calor de saída, o COP e a taxa de da exergia destruída.

Iremos assumir que este processo está em regime permanente desde que não acorra variação com o tempo. A variação da energia cinética e potencial são desconsiderados.

As propriedades de entrada e saída serão determinadas perante sua temperatura e pressão, retirado da tabela 13a.

De entrada:

Temos:

Para saída:

Temos:

a) Determinando o calor rejeitado:

b)Determinando COP, pela definição temos: