Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 178
Uma máquina térmica cuja eficiência é de utiliza um reservatório quente a e um reservatório frio a . Calcule a variação da entropia dos dois reservatórios quando de calor é transferido do reservatório quente para a máquina. Essa máquina satisfaz o princípio de aumento da entropia? Caso a eficiência da máquina térmica seja aumentada para o princípio de aumento da entropia ainda será satisfeito?
Passo 1
Hey hey, vamo lá! A fonte e a temperatura da pia e a eficiência térmica. de um motor térmico são dadas. A mudança de entropia dos dois reservatórios deve ser calculada e deve ser determinado se este motor satisfaz o princípio do aumento da entropia.
Passo 2
Analisando, de acordo com a primeira lei e a definição de eficiência térmica,
quando a eficiência térmica é de 40%. A mudança de entropia de tudo envolvido no processo é:
Passo 3
Como a entropia de tudo é aumentado, esse motor é possível. Quando a eficiencia térmica do motor é 70%,
A mudança total da entropia é então
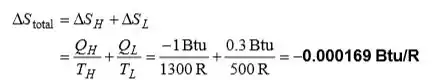
o que é uma diminuição da entropia de tudo o que está envolvido com este motor. Portanto, este motor é agora impossível.