Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 66
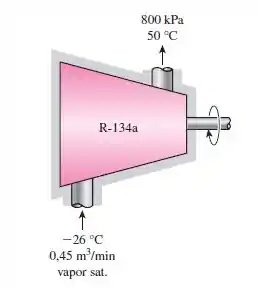
Refrigerante-134a entra em um compressor adiabático a como vapor saturado a uma taxa de , saindo a e . Determine o consumo de potencia no compressor, a eficiencia isentropica do compressor e a taxa de destruição de exergia e a eficiencia de segunda lei do compressor. Considere .
Passo 1
Temos um refrigerante entrando em um compressor e temos que determinar a energia reversível, a eficiência isentrópica e a taxa da exergia destruída.
Assumindo que este processo está em regime permanente, desde que não há mudança pelo tempo. Considerando a variação da enérgica cinética e potencial insignificantes. Pelo dispositivo ser adiabático isto implica que transferência de calor ira ser desconsiderado.
Determinando a propriedades de entrada e saída do sistema:
De entrada:
Olhando na tabela R-134a, temos:
Para saída:
Temos:
E para variáveis:
Temos:
a)
Para determinar a energia atual de entrada do compressor, vamos determinar o fluxo de massa e assim utilizaremos a formula da energia.
Aplicando a formula da energia:
Passo 2
b)
Para determinarmos a eficiência isentrópica precisamos determinar a energia isentrópica.
Aplicando a formula de eficiência isentrópica:
Passo 3
c) aplicando fórmula de exergia destruída temos:
Calculando a energia reversível para poder aplicar a segunda lei da eficiência:
Aplicando a segunda Lei da eficiência:
Resposta
a)
b)
c)