Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 15.Problemas - Ex. 111
Repita o Prob. 15–109, usando o metano ( (g)) como combustível em vez do álcool metílico.
Passo 1
Entendendo o problema:
O processo para este problema é exatamente o mesmo destrinchado no problema 109, sob as mesmas condições, mas mudando o combustível para o metano . Como no problema anterior, são analisadas duas condições de operação da combustão: a pressão constante e o volume constante.
A equação de combustão estequiométrica do metano é dada por:
Com o coeficiente determinado pelo balanço de massa para o
Assim, a equação de combustão torna-se:
Passo 2
(item a): Sistema a volume constante
O sistema é fechado, sob condições de combustão adiabática (Q=0) e sem interações por trabalho (W=0). O M balanço de energia se deve somente as entalpias de produtos e reagentes, dado por:
(1)
Como reagentes e produtos são gases ideais (PV=RT)
(2)
Com os reagentes no estado padrão, e usando os dados da tabela da figura 1:
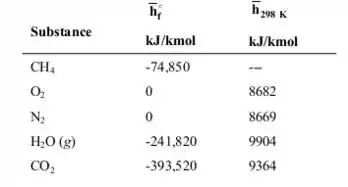
Figura 1: dados de entalpia de formação e entalpia no estado padrão para os componentes do processo de combustão
Aplicando a equação (2):
Que leva a seguinte expressão:
Novamente utilizado a estratégia de tentativa e erro, testando um valor de temperatura e seus respectivos valores de entalpia tabelados para as substâncias da equação (3), o valor de temperatura é obtido é
Como produtos e reagentes são gases ideais, a pressão máxima que pode ocorrer na câmara na temperatura de chama é calculada como:
Passo 3
Processo a pressão constante.
Para este caso, novamente, a equação de combustão é a mesma que para o processo a volume constante. Entretanto o balanço de energia se modifica contabilizando somente os termos das entalpias, uma vez que os termos associados ao trabalho na fronteira são combinados com os termos associados a energia interna. Assim, o balanço fica:
(4)
Aplicando (4) a equação de combustão:
Que gera:
Que obtêm uma temperatura de chama novamente, tratando os gases de produtos e reagentes como gases de volumes ideais o volume máximo na á pressão constante é:
Resposta
Ei, a resposta está no passo a passo :)