Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 143
Repita o Prob. 5–142, considerando agora que a linha é preenchida com ar e mantida a 2.000 kPa e 327 °C.
Passo 1
Entendendo o problema:
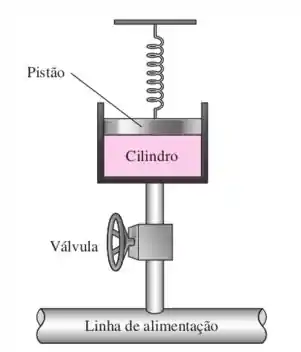
Para esse problema, consideramos o cilindro como sendo o sistema. Este é preenchido com vapor cuja temperatura e pressão são conhecidas. O cilindro possui sua pressão interna variando de acordo com o volume, devido a um dispositivo mola-pistão acoplado. Quando a válvula é aberta, o vapor escoa para o cilindro, até que a pressão interna seja igual a pressão da linha de alimentação. O problema então demanda qual a temperatura do estado final, quando a pressão no cilindro se iguala a pressão da linha de alimentação
Considerações:
- O processo é adiabático, ou seja, não há trocas de calor durante o enchimento do cilindro
- O volume de controle assumido é o volume interior do cilindro
- Uma vez que massa cruza este volume de controle durante o enchimento, com suas condições de volume e pressão variando durante o processo, este é transiente.
- Deve-se ter em mente que a energia associada ao fluido em escoamento é caracterizada pela entalpia
O primeiro passo é realizar os balanços de massa e energia para o sistema. Dessa forma:
Balanço de massa:
Uma vez que no início do processo não há vapor dentro do cilindro, 
. Então o balanço de massa se reduz a:
Balanço de energia:
A variação de energia do sistema é equacionada como:
Pelas considerações realizadas no balanço de massa, o balanço de energia se reduz a
Combinando os dois balanços:
Em que 
a energia interna do vapor no estado final, quando não há mais escoamento.
Passo 2
Calculando o volume do estado final e o trabalho produzido no processo:
O problema menciona que a pressão no cilindro é função do volume, controlada pela mola. É possível admitir então que a mola imprime uma variação linear entre a pressão e o volume. Assim 
são obtidos de acordo com os dados do enunciado:
E assim a relação entre pressão e volume é dada pela equação:
Como no estado final, a pressão é de 
, que é a pressão da linha de alimentação, o volume do estado final é
Com a expressão da pressão em função do volume, o trabalho realizado pelo processo, do estado inicial em que o volume de vapor no cilindro é zero até o estado final em que o volume atinge o valor calculado acima é dado pela integral a seguir:
Passo 3
Determinando a temperatura no estado final:
Considerando o ar como um gás ideal, a massa 
. Substituindo essa expressão no balanço de energia, juntamente com o valor de trabalho obtido:
sendo 
a temperatura do vapor que entra no cilindro, igual a linha de alimentação. Substituindo os valores:
Resolvendo para a temperatura, 
.
Resposta
Temperatura final: 