Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 34
Repita o para uma razão de compressão igual a .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Bom... Como nos foi dada a razão de compressão do ciclo, podemos aplicar diretamente na fórmula para encontrar a eficiência térmica.
Quando podemos utilizar as hipóteses de padrão a ar frio (valores de calores específicos constante à temperatura ambiente), a fórmula da eficiência térmica para o Ciclo Otto ideal, envolvendo a razão de compressão é:
Onde é a razão de compressão e .
Portanto é só substituir na equação:
Ou:
Passo 2
Também nos foi perguntada a taxa de calor fornecida caso o ciclo produzisse de potência.
Vamos lembrar o diagrama de um ciclo Otto ideal:
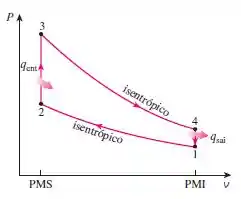
O calor fornecido será o calor que entra no sistema que é o que queremos saber.
A definição de eficiência de um sistema é dada pela razão daquilo que você produz pelo que você gasta.
No caso o que nós gastamos no ciclo Otto é combustível, ou seja, o calor que entra. O que produzimos é o trabalho de eixo ou .
Portanto:
Se sabemos a eficiência do sistema e o trabalho gerado (Potência), podemos então descobrir a taxa de calor que foi fornecida.