Um reservatório de pressão rígido isolado contém 1 kmol de ) a e 1 bar reservatório de pressäo é concctado por uma válvula a um grande reservatório de pressāo que contém a e 4 bar . Uma quantidade de nitrogênio flui para o reservatório de pressăo. gerando uma mistura argônio-nitrogènio à temperatura e a pressăo . Represente graficamente teórico mínimo na entrada de energia versus y , a fração molar de
Passo 1
Os dados são fornecidos para um dispositivo operando em estado estacionário que separa um gás natural em componentes. O exercício pede para plotarmos: Plote o teórico mínimo na entrada de energia versus y , a fração molar de
Temos os seguintes dados:

Passo 2
PREMISSAS: (1) O volume de controle mostrado na figura a seguir opera isotermicamente e em estado estacionário. (2) Os efeitos da energia cinética e potenciol podem ser ignorados. (3) Princípios de gás ideais aplicam-se aos componentes puros. A mistura segue o modelo Dalton.
ANÁLISE: A taxa de fluxo de massa em 1 é obtida usando a taxa de fluxo volumétrica dada e a equação de estado do gás ideal:
Em que
Taxa de fluxo molar
(1)
Passo 3
Com as premissas 1 e 2, um balanço da taxa de energia reduz
Uma vez que T1 = T2 = T3, o termo sublinhado desaparece, deixando
Um equilíbrio da taxa de entropia reduz no estado estacionário
ou, após o rearranjo e inserção
Nesta equação (- WWCV) está a entrada de trabalho. Como σtv≥0, segue-se que (-Wer) é mínimo quando σ ev = 0. De acordo.
- em
(2)
Passo 4
As equações governantes são as Equações (1) e (2).
(3)
Eq (3) pode ser plotada usando software de plotagem disponível. O resultado usando π é apresentado a seguir.
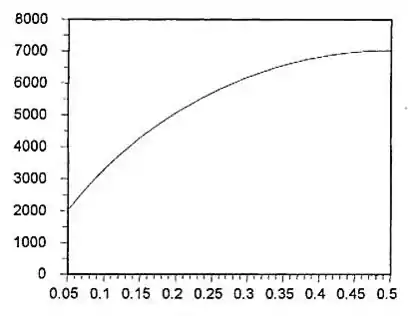
vemos a partir da plataforma que a força de movimento é necessária à medida que a fração molar de C2H6 aumenta.
Devido às inevitáveis irreversibilidades, o poder real requerido excederia o valor teórico mínimo obtido por exemplo (3).