Responda se cada uma das afirmativas é verdadeira ou falsa. Explique.
(a) O corolário da segunda lei de Carnot estabelece que todos os ciclos de potência operando entre os mesmos dois reservatórios têm a mesma eficiência térmica.
(b) Quando deixados sozinhos, os sistemas tendem a sofrer alterações espontâneas até alcançar o equilíbrio, tanto internamente quanto com sua vizinhança.
(c) Os processos internamente reversíveis não ocorrem realmente, mas servem como casos limites hipotéticos conforme as irreversibilidades internas são reduzidas cada vez mais.
(d) A energia de um sistema isolado permanece constante, mas sua entropia pode apenas decrescer.
(e) O coeficiente de desempenho máximo de qualquer ciclo de refrigeração operando entre reservatórios térmicos frio e quente a e , respectivamente, é aproximadamente .
Passo 1
a) O corolário da segunda lei de Carnot estabelece que todos os ciclos de potência operando entre os mesmos dois reservatórios têm a mesma eficiência térmica.
Vamos analisar com calma de acordo com os próprios corolários.
C1) “A eficiência térmica de um ciclo irreversível é SEMPRE MENOS do que a eficiência de um ciclo reversível operando entre os mesmos dois reservatórios.”
Isso se dá pelo seguinte:
O trabalho produzido por um ciclo IRREVERSÍVEL é sempre MENOR do que o trabalho de um ciclo REVERSÍVEL.
C2) “Todos os sistemas entre os mesmos dois reservatórios têm a mesma eficiência.”
Se houvessem dois ciclos REVERSÍVEIS dentro do mesmo reservatório com eficiências diferentes um do outro, indicaria que um teria mais irreversibilidades do que o outro fazendo com que
Isso gera um paradoxo, pois os ciclos já foram denotados como reversíveis, possuindo, portanto, a mesma eficiência térmica.
a) Afirmativa VERDADEIRA.
Passo 2
b) Quando deixados sozinhos, os sistemas tendem a sofrer alterações espontâneas até alcançar o equilíbrio, tanto internamente quanto com sua vizinhança.
Objetos como sistema e vizinhança atingem o equilíbrio quando suas entropias somadas chegarem ao ponto máximo, onde haverá o fim da variação de entropia.
Ocorre por conta da relação da Desigualdade de Clausius numa escala temporal. “Todo diamante vai virar grafite”, mas ninguém disse quando. Ou seja, o processo de equilíbrio VAI ACONTECER para TODOS OS SISTEMAS.
O momento de TEMPO, mencionado tem relação com o valor b e se refere a TODOS E QUAISQUER processos termodinâmicos.
A condição de equilíbrio diz sobre a presença de um processo REVERSÍVEL, sem nenhuma irreversibilidade e não impede o retorno do sistema ao momento IRREVERSÍVEL. Mas, tanto o sistema quanto a vizinhança devem retornar às suas condições iniciais.

É, acontece assim mesmo com o seu, o meu e o nosso cafezinho. Logo:
b) Afirmativa VERDADEIRA.
Passo 3
c) Os processos internamente reversíveis não ocorrem realmente, mas servem como casos limites hipotéticos conforme as irreversibilidades internas são reduzidas cada vez mais.

Se você conseguir seguir a tirinha, nas mesmas condições e no mesmo experimento, você consegue negar a afirmativa.
Caso não consiga, terá de se contentar com o fato de que para que seja possível um processo termodinamicamente reversível, por completo, é necessário que esse processo ocorra de modo INFINITESIMALMENTE DEVAGAR, fazendo com que TODAS AS INTERAÇÕES DO SISTEMA OCORRAM EM TEMPERATURA CONSTANTE.
Ou seja, IMPOSSÍVEL.
Lembrando que a consideração de reversibilidade do sistema está relacionada ao Ciclo de Carnot, fazendo deste um MODO PERFEITO DE EXECUÇÃO de um CASO–LIMITE, somente.
c) Afirmativa VERDADEIRA.
Passo 4
d) A energia de um sistema isolado permanece constante, mas sua entropia pode apenas decrescer.

Como pode né?
Uma ÚNICA ‘AFIRMAÇÃO’ DESTRUIR TUDO no ÚLTIMO EXERCÍCIO DO CAPÍTULO, que foi estudado com afinco e dedicação totais suas e por cientistas renomados que se dedicaram a concluir essas leis e obras sobre Termodinâmica.
Caso não tenha ficado claro, a gente refresca a sua memória. De acordo com TODO O CAPÍTULO 5, vimos que:
É IMPOSSÍVEL, PARA QUALQUER SISTEMA, OPERAR DE MODO A DESTRUIR A ENTROPIA
Isso se dá, inclusive pela análise da Desigualdade de Clausius quando esta menciona que:
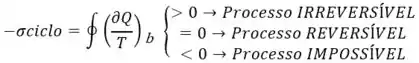
d) Afirmativa FALSA.
Passo 5
e) O coeficiente de desempenho máximo de qualquer ciclo de refrigeração operando entre reservatórios térmicos frio e quente a e , respectivamente, é aproximadamente .
Aqui vale a pena lembrar de um conceito antigo, lá do ensino médio, de conversão de temperaturas em escala termométrica.
Como, no problema, temos os valores em , temos que convertê-los para escala Kelvin onde:
O que gera:
Com isso, vamos às contas.
Lembrando que, por ser absoluta, o valor em Kelvin não será fornecido em grau (não há comparação).
e) Afirmativa VERDADEIRA.
Resposta
a) Afirmativa VERDADEIRA.
b) Afirmativa VERDADEIRA.
c) Afirmativa VERDADEIRA.
d) Afirmativa FALSA.
e) Afirmativa VERDADEIRA.