Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 140
Qual seria a modificação no impulso do Prob. 9–139E, considerando que o diâmetro da hélice é reduzido para 8 pés enquanto se mantém a mesma vazão mássica através do compressor. Nota: a razão entre os fluxos de massa já não será 20.
Passo 1
Vamos assumir que:
Existem condições operacionais estáveis.
As premissas do padrão aéreo são aplicáveis.
O ar é um gás ideal com aquecimentos específicos constantes à temperatura ambiente.
A saída de trabalho da turbina é igual à entrada de trabalho do compressor.
Sabemos que as propriedades do ar à temperatura ambiente são
O trabalho nos dois processos isentrópicos do ciclo gera
Passo 2
Bom, vamos observar a figura:
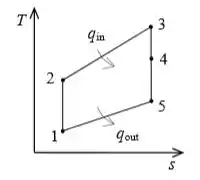
Como o trabalho produzido pela expansão 3-4 é igual ao usado pela compressão 1-2, um balanço energético fornece:
A taxa de fluxo de massa através da hélice é:
Passo 3
Agora, de acordo com o problema anterior
O excesso de entalpia gerado pela expansão 4-5 é usado para aumentar a energia cinética do fluxo através da hélice, então:
que quando resolvido pela velocidade com que o ar sai da hélice, chegamos em:
A força de empuxo gerada por esta hélice é então