Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 10.Problemas - Ex. 22

Um sistema de refrigeração por compressão de vapor tem uma capacidade de 10 TR(35,2 kW) admite, na entrada do compressor, o Refrigerante 134a em forma de vapor superaquecido a 15ºC e 4 bar, enquanto na saída o valor é de 12 bar. O processo de compressão pode ser modelado por pv1,01 = constante. O condensador é resfriado a água, que entra a 20°C e sai a 30°C, com variação de pressão desprezível. A transferência de calor no exterior do condensador pode ser desprezada, Determine:

(a) a vazão mássica do refrigerante, em kg/s.

(b) a potência de acionamento e a taxa de transferência de calor do compressor, em kW.

(c) o coeficiente de desempenho.

(d) a vazão mássica da água de resfriamento, em kg/s.

(e) as taxas de produção de entropia no condensador e na válvula de expansão, em kW/K.

(f) as taxas de destruição de exergia no condensador e na válvula de expansão, cada uma expressa como uma porcentagem da potência do compressor. Assuma T0 = 20°C.

Passo 1

Saalve, tranquilo?

Vamos resolver juntos mais uma questão de termodinâmica?!

Passo 2

É dado que:

  • Capacidade do refrigerante: Q ˙ e n t = 10   t o n = 35,166   k W
  • Temperatura na entrada do compressor: T 1 = 15 ° C
  • Pressão na entrada do compressor: p 1 = 4   b a r
  • Pressão na saída do compressor: p 2 = 12   b a r
  • Pressão na saída do condensador: p 3 = 11,6   b a r
  • Temperatura na saída do condensador: T 3 = 44 ° C
  • Temperatura inicial da água: T c w , e n t = 20 ° C
  • Temperatura final da água: T c w . s a i = 30 ° C

O diagrama T - s é mostrado abaixo

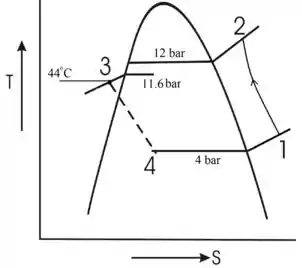
Passo 3

A pressão de p 1 = 4   b a r e T 1 = 15 ° C das tabelas de R134a superaquecido

h 1 = 258,155   k J / k g

s 1 = 0,93485   k J / k g ⋅ K

v 1 = 0,05258   m 3 / k g

O processo 1-2 segue a lei p v 1,01 = c t e .

p 1 v 1 1,01 = p 2 v 2 1,01 → 4 ⋅ 0,005258 1,01 = 12 ⋅ v 2 1,01

∴ v 2 = 0,017718   m 3 / k g

Passo 4

A pressão de p 2 = 12   b a r e v 2 = 0,017718   m 3 / k g das tabelas de vapor superaquecido, por interpolação

h 2 = 275,52 + 287,44 - 275,52 0,017718 - 0,01712 0,01835 - 0,01712 = 281,315   k J / k g

s 2 = 0,9164 + 0,9527 - 0,9164 0,017718 - 0,01712 0,01835 - 0,01712 = 0,93404   k J / k g ⋅ K

Passo 5

No estado 3 está no estado compressível

h 3 = h f = 112,22   k J / k g

s 3 = s f = 0,4054   k J / k g ⋅ K

h 3 = h 4

Passo 6

A pressão de p 4 = 4   b a r das tabelas de saturada

h f = 62   k J / k g

h f g = 190,32   k J / k g

s f = 0,2399   k J / k g ⋅ K

s g = 0,9145   k J / k g ⋅ K

Já que h 3 = h 4

h 3 = h f + x 4 h f g → 112,22 = 62 + x 4 ⋅ 190,32

∴ x 4 = 0,26387

E temos que

s 4 = s f + x 4 s f g = 0,2399 + 0,26387 0,9145 - 0,2399 = 0,4179   k J / k g ⋅ K

Passo 7

a) a taxa de vazão mássica do refrigerante

m ˙ = Q ˙ e n t h 1 - h 4 = 35,166 258,155 - 112,22

∴ m ˙ = 0,2409   k g / s

Passo 8

b) a potência de entrada do compressor

W ˙ C = m ˙ n n - 1 p 1 v 1 - p 2 v 2 = 0,2409 1,01 1,01 - 1 400 ⋅ 0,05258 - 1200 ⋅ 0,0177183

∴ W ˙ C = - 5,5951   k W

O sinal negativa indica que a potência entra para o compressor

A taxa de transferência de calor é dada por

Q ˙ C = W ˙ C + m ˙ h 2 - h 1 = - 5,5951 + 0,2409 281,315 - 258,155

∴ Q ˙ C = - 0,011756   k W

Passo 9

c) o coeficiente de performance

β = Q ˙ e n t W ˙ C = 35,166 5,5951

∴ β = 6,285

Passo 10

d) a taxa de vazão mássica da água resfriando

m ˙ c w h c w , s a i - h c w , e n t = m ˙ h 2 - h 3 = m ˙ c w h f , 30 ° C - h f , 20 ° C á g u a = m ˙ h 2 - h 3

→ m ˙ c w 125,79 - 83,96 = 0,2409 281,578 - 112,22

∴ m ˙ c w = 0,9753   k s / s

Passo 11

e) a destruição de exergia no condensador

E ˙ d c o n d e n s a d o r = T 0 σ d c o n d e n s a d o r = T 0 m ˙ s 3 - s 2 + m ˙ c w s c w , s a i - s c w , e n t

→ E ˙ d c o n d e n s a d o r = T 0 m ˙ s 3 - s 2 + m ˙ c w s f , 30 ° C - s f , 20 ° C

→ E ˙ d c o n d e n s a d o r = 293 0,2409 0,405 - 0,93404 + 0,9753 0,4369 - 0,2966

∴ E ˙ d c o n d e n s a d o r = 2,7509   k W

a destruição de exergia na válvula

E ˙ d v a l v u l a = T 0 σ d v a l v u l a = T 0 m ˙ s 4 - s 3 = 293 ⋅ 0,2409 0,4179 - 0,4054

∴ E ˙ d v a l v u l a = 0,8822   k W

Passo 12

a taxa de destruição de exergia no condensador como uma porcentagem de potência de entrada

% c o n d e n s a d o r = E ˙ d c o n d e n s a d o r W ˙ C = 2,7509 5,5951

∴ % c o n d e n s a d o r = 49,16 %

a taxa de destruição de exergia na válvula como uma porcentagem de potência de entrada

% v a l v u l a = E ˙ d v a l v u l a W ˙ C = 0,8822 5,5951

∴ % v a l v u l a = 15,76 %

Resposta

a) m ˙ = 0,2409   k g / s

b) Q ˙ C = - 0,011756   k W

c) β = 6,285

d) m ˙ c w = 0,9753   k s / s

e) % c o n d e n s a d o r = 49,16 % e % v a l v u l a = 15,76 %

Ver Outros Exercícios desse livro