Uma sonda interplanetária esférica, carregada eletronicamente, de 0,5 m de diâmetro, em regime permanente, transfere energia por radiação de sua superfície externa a uma taxa de 150 W. Se a sonda não recebe radiação do Sol ou do espaço, qual é a temperatura da superfície, em K? Considere
Passo 1
Fala galera! Tranquilo? Vamos começar essa questão interplanetária!
Primeiro, vamos dar uma desenhada nessa tal sonda esférica:
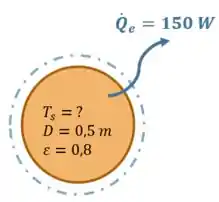
Bem bonita né? Vamos em frente!
Para cálculos que envolvem a taxa na qual a energia é emitida por radiação a partir de uma superfície, nós podemos usar aquela fórmula que é uma forma modificada da Lei de Stefan-Boltzmann:
Opa! Antes de calcularmos tudo, tá faltando o e a área A, não é?
O é a constante de Stefan-Boltzmann! E ela vale .
Mas e a área? A área que utilizamos aqui é a área superficial da esfera, ou seja, a área da casca esférica que envolve essa esfera!
Então:
Se ligou? Vamos partir para os cálculos então!
Passo 2
Já temos a nossa equação e todos os dados:
Mas nós queremos saber quem é , né? Então vamos isolá-lo:
Agora é só substituir os dados. Moleza!
Nesse caso, como a temperatura 0 K é o zero absoluto, não vamos utilizar os resultados negativos da equação, apenas o positivo, beleza?
Por aqui terminamos! Vamos partir para a próxima questão!