Suponha que uma linha reta ligue os pontos: e o ponto crítico no diagrama de em função . Essa linha será tangente a uma isotérmica numa pressão baixa.

Qual será a temperatura reduzida correspondente a essa isotérmica para a equação de Van der Waals?

Repita a parte para a equação de estado de Redlich-Kwong.

(Veja a nota apresentada no prob. 13.56)

E aí bonit@s, como vocês estão? Prontos pra mais uma questão maneira?

Se liguem só, para representar nosso problema vamos tomar o seguinte diagrama como referência

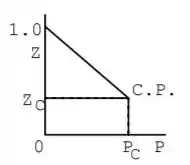
Temos que a inclinação para esse gráfico é dada por

Mas para temos que essa inclinação é igual a

Dessa forma teremos

Usando a solução do problema do livro vamos ter

Agora vamos substituir os valores das nossas constantes

Substituindo e simplificando nossa equação chegamos em

Resolvendo a equação do segundo grau e desprezando a raíz negativa vamos encontrar .