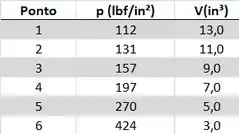
A tabela a seguir fornece dados medidos para a pressão versus o volume durante a compressão de um refrigerante no cilindro de um compressor em um sistema de refrigeração. Utilizando os dados da tabela, complete o seguinte:
a) Determine um valor de n tal que os dados sejam ajustados para uma equação do tipo
b) Calcule analiticamente o trabalho realizado sobre o refrigerante, em Btu, utilizando a equação em conjunto com o resultado do item (a).
c) Utilizando a integração gráfica ou numérica dos dados, calcule o trabalho realizado sobre o refrigerante, em Btu.
d) Compare os diferentes métodos para a estimativa do trabalho utilizados nos itens (b) e (c). Por que são estimativas?
Passo 1
Você sabe como um cilindro de um compressor funciona? Se não souber, não tem problema! Aqui está o esquema de compressão do refrigerante no cilindro:
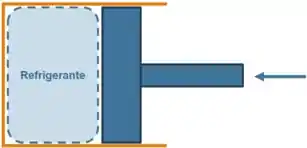
O embolo da direita vai comprimir o fluido exatamente como mostram os dados da tabela. O restante do enunciado não nos deu tantas informações né? Então vamos com calma, seguindo o passo-a-passo!
Passo 2
Na letra (a), temos que calcular o n da equação . Vamos chamar essa constate de c para facilitar um pouco. Então:
Você concorda comigo que se mantermos esse n no expoente do V vai ser bem complicado para isola-lo? Então vamos aplicar o logaritmo dos dois lados da equação para descer esse n!
Beleza! Agora está bem mais fácil de isolar esse bendito n.
Vamos partir para a tabela dada no enunciado. Vamos pegar os dados do ponto 1 e do ponto 6 e aplicar na nova equação que achamos!
Igualando as equações teremos:
Passo 3
Já na letra (b), vamos utilizar alguns resultados da letra (a).
Temos que , certo? Vamos reescrever da seguinte forma:
Mas por que escrever assim? Lembra que o enunciado da letra (b) nos pediu para usar a fórmula ? Vamos substituir esse p da fórmula pelo nosso p! E vamos avaliar durante todo o processo de compressão, ou seja, do ponto 1 ao ponto 6.
Vamos ter então:
Vamos botar a mão na massa e integrar então!
E esse c aí que não sabemos quanto vale? A gente o substitui pela primeira equação !
Agora tá fácil né? Só os dados com os da tabela e o n pelo que a gente achou no item (a).
Falta só mais uma coisinha! O trabalho foi pedido em Btu, então pra converter de para Btu, basta multiplicarmos por 0,00011.
Passo 4
Agora para uma integração gráfica da letra (c) temos que plotar um gráfico p x V daquela tabela!
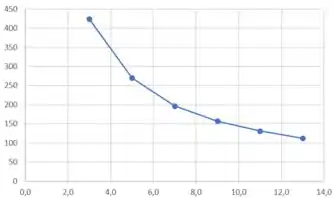
Lembra que Cálculo Diferencial e Integral a gente pode calcular a integral aproximada de um gráfico desenhando retângulos e depois somando as áreas desses retângulos? Isso que nós vamos fazer aqui.
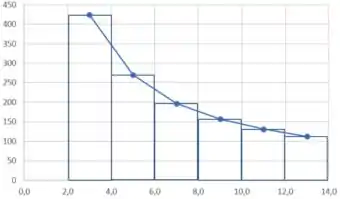
Cada retângulo tem como base 2 in³ e para cada altura são os valores de pressão em lbf/in² que nos foram dados na tabela do enunciado!
Somando as áreas temos:
Que passando para Btu fica igual à .
Passo 5
Opa! Calculamos o mesmo trabalho, mas obtivemos dois valores diferente. E agora?
Pode ficar tranquilo que essa diferença se dá devido à aproximação de retângulos no desenvolvimento da letra (c). Mas percebe que mesmo diferentes, os valores são próximos? Por isso podemos utilizar como estimativa!
Resposta
a) n = 0,9
b) W = - 0,2024 Btu
c) W = - 0,2884 Btu