Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 13.Problemas - Ex. 43

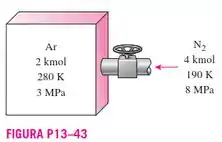
13 - 43 Um tanque rígido contém 2   k m o l de gás argônio a 280   K e 3   M P a . Uma válvula é então aberta, e 4   k m o l de gás N 2 entram no tanque a 190   K e 8   M P a . A temperatura da mistura final é de 230   K . Determine a pressão da mistura usando ( a ) a equação de estado do gás ideal e ( b ) o diagrama de compressibilidade e a lei de Dalton.

Passo 1

Bora começar pela letra (a)

Antes e depois temos:

P 1 V 1 = n 1 R u T 1 ⇒     R u = P 1 V 1 n 1 T 1

P 2 V 2 = n 2 R u T 2   ⇒     R u = P 2 V 2 n 2 T 2

Como:

R u = R u

P 1 V 1 n 1 T 1 =   P 2 V 2 n 2 T 2  

P 1 V 1 n 2 T 2 n 1 T 1 V 2 = P 2

Mas os volumes são os mesmos:

P 1 n 2 T 2 n 1 T 1 = P 2

3   M P a 4 + 2 k m o l ⋅ 230 ° K 2   k m o l ⋅ 280 ° K = P 2

P 2 = P m = 7,39   M P a

Passo 2

Agora a letra (b)

Esse método é mais complicado, precisaremos dividir em antes e depois da mistura.

Antes da mistura

Precisaremos usar a F I G U R A   A - 15 , pág 932.Para isso, precisamos saber a temperatura e pressão crítica do a r , elas são:

T c r , A r = 151 ° K         e       P c r , A r = 4,86 M P a

Então calculamos um T R e um P R   ( T   e   P   R e l a t i v o s ) :

T R = T 1 T c r , A r = 280 ° K 151   ° K = 1,854

P R = P 1 P c r , A r = 3   M P a 4,86 M P a = 0,6173

Agora olhamos na F I G U R A   A - 15 , pág. 932 no primeiro gráfico, o P R é o e i x o   x e o T R são as linhas rosas continuas, o que queremos é o fator de compressibilidade Z , que está no e i x o   y , no nosso caso com nossas referências ele vai bater em:

Z a r ≅ 0,985

Agora podemos usar esse Z a r para calcular um volume V (não confundir com volume especifico). Usamos uma generalização de P V = n R T :

V = Z a r N a r R T P = 0,985 ⋅ 2 k m o l ⋅ 8,314 k P a ⋅   m 3 k m o l   K 3000   k P a = 1,529 m 3

Passo 3

Depois da mistura

Na mistura precisaremos trabalhar separado com o a r e com o N 2 , aqui o que buscarmos na F I G U R A   A - 15 , pág 93, é o P R   , que é o que a questão pede. Utilizaremos nesse caso o T R que já sabemos como calcula e o v r ( volume especifico) que é a linha rosa tracejada no gráfico:

Então:

Para o A r :

T R = T m T c r , A r = 23 0 K 151   K = 1,523

Lembrando que o volume será o mesmo antes e depois.

v R , A r = v A r R T P c r , A r   = V m N A r R T P c r , A r   = 1,529 m 3 2 k m o l 8,314   k P a ⋅ m 3 k m o l ⋅ K ⋅ 151 K 4860 k P a = 2,96

Com essas referências, para o a r :

P R = 0,496

Para o N 2 :

T R = T m T c r , A r = 230 K 126,2   K = 1,823

Lembrando que o volume será o mesmo antes e depois.

v R , N 2 = v N 2 R T P c r , N 2   = V m N N 2 R T P c r , N 2   = 1,529 m 3 4 k m o l 8,314   k P a ⋅ m 3 k m o l ⋅ K ⋅ 126,2 K 3390 k P a = 1,235

Com essas referências, para o N 2 :

P R = 1,43

Passo 4

Agora usamos a fórmula de P R

P R = P P c r

Logo:

P R , A r = P A r P c r , A r   ⇒     0,496 = P A r 4860 k P a ⇒ P A r = 2,41 M P a

P R , N 2 = P N 2 P c r , N 2 ⇒     1,43 = P N 2 3390 k P a ⇒ P N 2 = 4,85 M P a

Assim a Pressão final da Mistura vai ser:

P m   = P A r + P N 2

P m =   2,41 M P a +   4,85 M P a

E FINALMENTE:

P m = 7,26 M P a

Realmente um valor bem próximo do que tínhamos achado no Passo 1 de forma bem mais simples.

Resposta

a   P m = 7,39   M P a

b   P m = 7,26 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma mistura de gases consiste em 20 % de O 2 , 30 % de N 2 e 50 % de C O 2 em bases mássicas. Determine a análise volumétrica da mistura e a constante de gás aparente da mistura de gases.
Uma mistura de gases ideais também é um gás ideal? Dê um exemplo.
Determine as frações molares de uma mistura de gases que consiste em 75 % de C H 4 e 25 % de C O 2 em massa. Determine também a constante de gás da mistura de gases.
Considere uma mistura de dois gases A e B . Mostre que quando as frações mássicas m f a e m f b são conhecidas, as frações molares podem ser determinadas com:onde M A e M B são as massas molares de A
Uma mistura gasosa consiste em 3l b m o l de hélio, 1,5l b m o l de oxigênio, 0,3l b m o l de vapor de água e 2 , 5l b m o l de nitrogênio. Determine a fração molar dos vários constituintes e o pesomo