Um tanque rígido fechado contém água inicialmente a uma pressão de 20 bar, um título de 80%, e um volume de 0,5 m3, sendo essa resfriada até a pressão de 4 bar. Mostre o processo da água em um esboço do diagrama T–υ e calcule o calor transferido, em kJ.
Passo 1
Ooopa, beleza?
Vamos lá pra mais uma questão bem interessante de termodinâmica!
Passo 2
A água está sendo mandada em um tanque rígido de uma pressão para a outra. Então, o processo é isocórico. O diagrama vai ser uma linha reta de uma pressão constante de a pressão de .
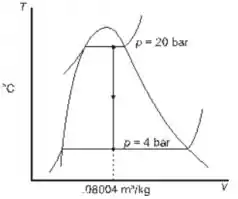
Passo 3
Para achar a transferência de calor, escreva a equação de balanço de energia
Já que a gente pode desconsiderar os efeitos de energia cinética e potencial e o trabalho não pode ser feito em um sistema rígido e fechado
Passo 4
Para achar a transferência de calor, primeiro achamos a mudança na energia interna. Para achar a energia interna, sabendo o valor dos volumes internos específicos. Então, obtemos os valores de volume específico e energia interna no estado 1 da Tabela A-3 “Propriedades de Água Saturada – Tabela de Pressão”. Em os valores são
Resolvendo para a energia interna específica no estado 1 usando a seguinte equação
Resolvendo para o volume específico usando a seguinte equação
Passo 5
Já que o processo é isocórico, volume específico inicial e final são iguais (). Obtendo os valores de volume específico em da Tabela A-3 “Propriedades de Água Saturada – Tabela de Pressão”
Já que o volume específico no estado 1 está entre . Isso significa que para achar a energia interna específica no estado 2, achamos as equações para título.
Passo 6
Resolvendo para o título no estado 2
Obtendo os calores de energia interna específica em da Tabela A-3 “Propriedades de Água Saturada – Tabela de Pressão”
Achando a energia interna específica no estado 2
Passo 7
Avaliando a massa usando a seguinte equação
Resolvendo para a transferência de calor
O sinal negativo significa que a transferência de calor ocorre a partir do sistema.