Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 150
Um tanque rígido isolado é dividido em dois compartimentos de volumes diferentes. Inicialmente, cada compartimento contém o mesmo gás ideal sob pressões idênticas, mas em temperaturas e massas diferentes. A parede que separa os dois compartimentos é removida, e os dois gases se misturam. Considerando calores específicos constantes, encontre a expressão mais simples para a temperatura da mistura, escrita na forma de
onde e são a massa e a temperatura da mistura final, respectivamente.
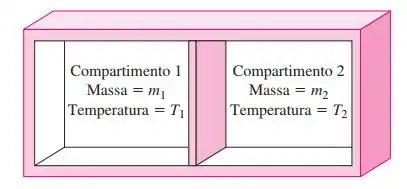
Passo 1
O sistema é formado pelos dois compartimentos. Como é isolado, consideramos que não há troca de calor, e por ser um tanque rígido, não há variação de volume, e o trabalho nesse caso é nulo. Assim, a equação de balanço de energia é:
Passo 2
A partir da equação de balanço de energia, temos:
Podemos considerar que , a temperatura final será: