Um tanque rígido e isolado equipado com um agitador contém água, inicialmente como uma mistura bifásica líquido-vapor a 20 lbf/in2 (137,9 kPa). Essa mistura consiste em 0,07 lb (0,03 kg) de água líquida saturada e 0,07 lb de vapor d’água saturado. Um agitador movimenta a mistura até que toda a água se torne vapor saturado a uma pressão maior do que 20 lbf/in2. Os efeitos das energias cinética e potencial são desprezíveis. Para a água, determine
(a) o volume ocupado, em ft3.
(b) a temperatura inicial, em °F.
(c) a pressão final, em lbf/in2.
(d) o trabalho, em Btu.
Passo 1
Saaalve, tranquilo?
Vamos lá pra mais uma questão bem interessante de termodinâmica!
Passo 2
É dado que, inicialmente:
- Pressão:
- Massa de líquido saturado:
- Massa de vapor saturado:
Passo 3
O diagrama é mostrado abaixo
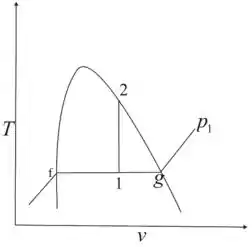
Passo 4
A gente sabe que o título da mistura é dado por
Então, no estado inicial
Passo 5
b) No estado inicial o sistema é líquido – região de vapor. Então, a temperatura é a temperatura de saturação. Logo, da tabela em
Passo 6
a) agora, podemos determinar o volume do sistema. Da tabela a gente consegue os valores de e no estado 1
Passo 7
c) No estado 2, já que a massa e o volume permanecem constantes
No estado 2, o sistema é vapor saturado, então da tabela para . Escrevendo os valores próximos a
- Em a pressão é
- Em a pressão é
- Em a pressão é
- Em a pressão é
Calculando a pressão final por interpolação
Passo 8
d) No estado 2, já que a massa e o volume permanecem constantes
No estado 2, o sistema é vapor saturado, então da tabela para . Escrevendo os valores próximos a
Calculando a energia interna específica final por interpolação
Passo 8
Considerando o balanço de energia para o sistema
Calculando a energia interna específica inicial
Calculando o trabalho feito para essa massa
Resposta
a)
b)
c)
d)