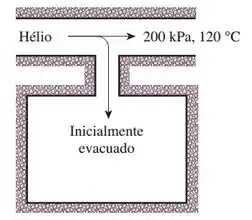
Um tanque rígido e isolado que inicialmente está vazio é conectado por meio de uma válvula a uma linha de alimentação que transporta hélio a 200 kPa e 120 °C. A válvula é aberta e o hélio

escoa para o tanque até que a pressão atinja 200 kPa; nesse instante, a válvula é fechada. Determine o trabalho de escoamento realizado pelo hélio da linha de suprimento e a temperatura final do hélio no tanque.

Achando o volume específico do Hélio utilizando a equação dos gases ideais:

Em que é a constante universal dos gases, T é a temperatura e P é pressão.

Substituindo , e na equação:

Calculando o trabalho do escoamento:

Substituindo e na fórmula acima:

Portanto o trabalho de escoamento é

Considerando que o trabalho do escoamento na linha de suprimento é convertido em energia interna sensível no tanque.

Podemos encontrar a temperatura do hélio igualando:

Sabendo que e