Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 3.Problemas - Ex. 73

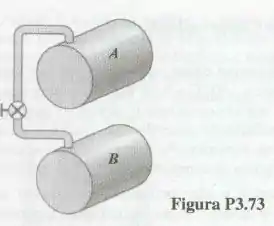
Um tanque rígido com volume de 1   m 3 contém propano a 100   k P a e 300   K e está conectado, através de uma tubulação com válvula, a outro tanque com volume de 0,5   m 3 que contém propano a 250   k P a e 400   K . A válvula é aberta e espera-se até que a pressão se torne uniforme. Sabendo que a temperatura final de equilíbrio é 325   K , determine a pressão no final desse processo.

Passo 1

Oi pessoal, tudo certo? Vamos analisar essa questão!

Primeiro, temos que avaliar se o propano pode ser considerado um gás ideal a partir das condições do enunciado. Analisando a tabela, temos que:

P c = 4,25   M P a

R = 0,1886   k J / k g ⋅ K

Como as pressões de trabalho P são bem menores que P c , podemos considerar o propano como um gás ideal, portanto:

P V = M R T

Passo 2

Vamos calcular a massa de cada tanque:

m 1 = P 1 V 1 R T 1

m 1 = 100 1 0,1886 300

m 1 = 1,767   k g

Para o segundo tanque, temos que:

m 2 = P 2 V 2 R T 2

m 2 = 25 0 0,5 0,1886 4 00

m 2 = 1,656   k g

Passo 3

A massa total será:

M = m 1 + m 2

M = 3,42   k g

O volume total será:

V = v 1 + v 2

V = 1 + 0,5 = 1,5   m 3

Portanto, a pressão total será:

P = M R T V

P = 3,42 0,1886 325 1,5

P = 139,75   k P a

Resposta

P = 139,75   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reconsidere o P r o b .3 – 76 . Usando o EES (ou outro programa), investigue o efeito do diâmetro do balão sobre a massa do hélio contido no balão para as pressões (a) 100k P a e (b) 200k P a . Varie
Determine o fator de compressibilidade para o estado onde a temperatura reduzida é 0,85 e o título é igual a 0,6 .
Calcule as constantes de gás perfeito do argônio e do hidrogênio utilizando os dados da Tab. A.2. Verifique seus resultados com os valores indicados na Tab. A.5.
Determine o volume ocupado por 2k g de etileno a 270K e 2500k P a . Utilize o diagrama de compressibilidade generalizado.
Considere um gás perfeito. Determine a variação percentual da pressão no gás num processo onde a massa e o volume permanecem constantes e o valor da temperatura absoluta é dobrado. Repita o problema a