Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 15.Problemas - Ex. 83

Um tanque de volume constante adiabático contém uma mistura de 1 kmol de gás de hidrogênio ( H 2 ) e a quantidade estequiométrica de ar a 25 °C e 1 atm. Em um dado momento, o conteúdo do tanque é incendiado. Considerando uma combustão completa, determine a temperatura final no tanque.

Passo 1

Vamos assumir que:

O tanque é adiabático.

Os reagentes e os produtos são gases ideais.

Não há interações de trabalho.

A combustão está completa.

Passo 2

A equação de combustão de H 2 com a quantidade estequiométrica de ar é

H 2 + 0.5 ( O 2 + 3.76 N 2 ) → H 2 O + 1.88 N 2

A temperatura final no tanque é determinada a partir da relação de balanço de energia\ E e n t - E s a í d a = Δ E s i s t e m a para reagir sistemas fechados sob condições adiabáticas ( Q = 0 ) sem interações de trabalho ( W = 0 ) .

∑ N R ( h ° ̄ f + h ̄ - h ° ̄ - P v ̄   ) R = ∑ N P ( h ° ̄ f + h ̄ - h ° ̄ - P v ̄   ) P

Como os reagentes e os produtos se comportam como gases ideais, toda a energia interna e entalpias dependem da temperatura somente e os termos P v _ nesta equação podem ser substituídos por R u T .

Então:

∑ N P ( h ° ̄ f + h ̄ T p - h ̄ 298 K - R u T   ) P = ∑ N R ( h ° ̄ f R u T ) R

uma vez que os reagentes estão à temperatura de referência padrão de 25 ° C. Das tabelas:

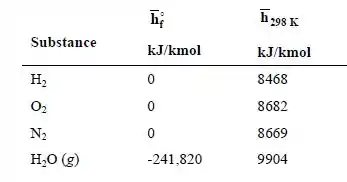
Então,

h ̄ H 2 O + 1.88   h ̄ N 2 - 23.94 × T P = 259,648   k J

A temperatura dos gases do produto é obtida a partir de uma solução de tentativa e erro,

Passo 3

À 3050K:

h ̄ H 2 O + 1.88   h ̄ N 2 - 23.94 × T P = 260,163   k J ( M a i o r   q u e   259,648   k J )

À 3000K:

h ̄ H 2 O + 1.88   h ̄ N 2 - 23.94 × T P = 255,089   k J ( M e n o r   q u e   259,648   k J )

Por interpolação:

T P = 3045   K

Resposta

T P = 3045   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tensão de cisalhamento na parede, τ w , em uma camada limite depende da distância a partir da borda de ataque do objeto, x , da massa específica, ρ , e da viscosidade, μ , do fluido e da velocidade
Um arranjo pistão-cilindro contém vapor de água superaquecido. Durante um processo adiabático real, a entropia do vapor aumentará (considere as opções: nunca, às vezes, sempre)?
Em velocidades relativamente muito altas, o arrasto sobre um objeto é independente da viscosidade do fluido. Desse modo, a força de arrasto aerodinâmico, F , sobre um automóvel é uma função somente da
Quais são os três mecanismos que podem causar a variação da entropia de um volume de controle?
A entropia do fluido de trabalho do ciclo ideal de Carnot aumenta, diminui ou permanece a mesma durante o processo isotérmico de adição de calor?