Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 14.Problemas - Ex. 144
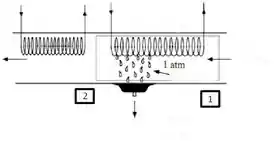
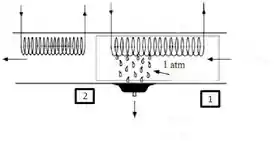
Ar úmido deve ser condicionado em um processo a uma pressão constante a de de bulbo seco e de umidade relativa para do ponto de orvalho e de umidade relativa. O ar escoa pelas serpentinas de resfriamento até que se remova toda a umidade necessária para atingir o teor de umidade final e, em seguida, escoa por serpentinas de aquecimento para atingir o estado final. O fluxo de ar seco é de .
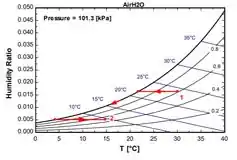
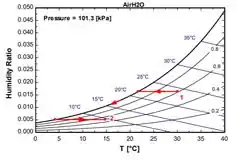
Faça um desenho esquemático do sistema e o diagrama psicrométrico do processo.
Determine a temperatura do ponto de orvalho e vazão volumétrica da mistura que entra nas serpentinas de resfriamento.
Qual é a taxa líquida de transferência de calor para todo o processo, em ?
Passo 1
Antes de partirmos para a resolução propriamente dita vamos fazer algumas considerações que são:
- Este é um processo de fluxo constante e, portanto, a vazão mássica do ar seco permanece constante durante todo o processo.
- Ar seco e vapor de água são gases ideais.
- As mudanças de energia cinética e potencial são insignificantes.
Pois bem, agora conseguimos fazer um desenho esquemático do sistema mencionado na questão e o diagrama psicrométrico, para esse vamos utilizar o EES colocando os dados da questão. Dessa forma, o esquemático e o diagrama ficam sendo
Passo 2
Dando prosseguimento à resolução da questão teremos que os estados de entrada e saída do ar são completamente especificados e a pressão total é de . As propriedades do ar nos estados de entrada e saída são determinados a partir da tabela psicrométrica como
Além do que temos, ainda, os seguintes dados que podem ser extraídos
Temos ainda que
A vazão do volume na entrada será então
Passo 3
Por fim, para concluirmos o exercício devemos lembrar que podemos aplicar as equações do balanço de massa para a água e o balanço de energia na seção combinada de resfriamento e desumidificação teremos
Do balanço de energia temos
Resposta
