Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 61
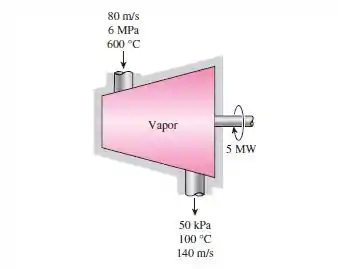
Vapor de agua a , e entram em uma turbina adiabática e sai a , e . Considerando que a potencia produzida pela turbina e de , determine a potencia reversível e a eficiencia de segunda lei da turbina. Considere que a vizinhança esta a .
Passo 1
Temos vapor de água passando por uma turbina adiabática e temos que determinara a potencia mínima ou reversível e a segunda lei da eficiencia na turbina.
Assumindo que este processo está em regime permanente, pois, não ocorrer variações em função do tempo. A variação da energia potencial é desconsiderada. A temperatura ambiente ou das vizinhanças é .
Coletando os dados de entrada e saída da tabela A-4 e A-6, temos:
Temos:
Para saída:
Temos:
Temos todas as propriedades para seguirmos com os cálculos, vamos lá!
Passo 2
a)Como a turbina será um dispositivo de controle de volume e constante poderemos descrever as equações de balanço energético de outra forma.
Devido ser um sistema de controle de volume a taxa de variação de energia permanece igual na entrada e saída.
Portanto:
Substituindo os valores poderemos determinar o fluxo de massa, informação está que será utilizada para calcular a quantidade de trabalho reversível.
Como o sistema é de controle de volume e regime permanente podemos escrever a equação de balanço da seguinte forma:
Como a exergia destruída é igual à zero, pois é reversível neste caos e a variação da exergia tende a zero, pois estamos em regime permanente. Temos:
Note que será igual à zero, pois consideramos a variação deste como insignificante.
Substituindo valores, temos:
Passo 3
b)Como obtemos a taxa de energia de saída e reversível de saída podemos aplicara segunda lei de eficiência na turbina:
Resposta
a)
b)