Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 9.Problemas - Ex. 57
57 Uma turbina, que opera com amônia, é utilizada num ciclo térmico de refrigeração. A pressão e a temperatura na seção de alimentação da turbina são iguais a 2,0 MPa e 70°C. Esta turbina aciona um compressor de amônia que é alimentado com vapor saturado de amônia que é alimentado com vapor saturado de amônia a -20°C. As pressões de exaustão nos dois equipamentos são iguais a 1,2 MPa e as duas exaustões são misturadas. Alega-se que a razão entre a vazão em massa que escoa na turbina e a vazão em massa total (soma da vazão em massa no compressor com a vazão na turbina) é igual a 0,62. Como você julga esta alegação? É possível realizar tal processo?
Passo 1
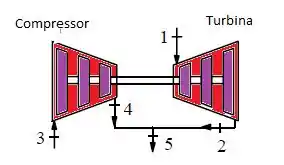
Nessa questão vamos usar a equação da continuidade:
A equação da energia:
E da equação da entropia:
Ahhh.. e as tabelas do final do livro..
Passo 2
Vamos começar fazendo uma pequena mágica: (que é o 0,62)
Então ficamos com a equação da energia:
E a equação da entropia:
Passo 3
No estado 1 temos amônia superaquecido, então pegamos os dados na tabela B.2.2:
E no estado 3 temos vapor saturado:
E no estado 5 podemos calcular a entalpia:
Agora a gente procura na parte de 1200 kPa, na tabela B.2.2 essa entalpia. E ta bem na linha de 40°C certinho e bonitinho. Então pegamos a entropia:
Passo 4
Usando a equação da entropia:
Como é netagivo, então é impossível.
Resposta
Impossível