Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 74
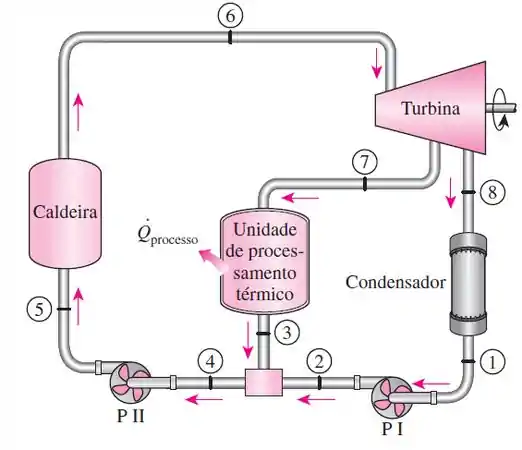
Vapor de água entra na turbina de uma usina de cogeração a 7 MPa e 500 °C. Um quarto do vapor é extraído da turbina à pressão de 600 kPa para uma umidade de processamento térmico. O restante do vapor continua se expandindo até 10 kPa. Ao sair da turbina, o vapor é condensado e misturado à água de alimentação a uma pressão constante, e a mistura é bombeada até a pressão da caldeira, igual a 7 MPa. O fluxo de massa do vapor na caldeira é de 30 kg/s. Desprezando quedas de pressão e perdas de calor na tubulação, e considerando que a turbina e a bomba sejam isentrópicas, determine a potência líquida produzida e o fator de utilização da usina.
Passo 1
Tá legal! A primeira coisa que devemos fazer é pegar as propriedades do fluido nos pontos de interesse com os dados fornecidos no enunciado, então, com a ajuda das tabelas termodinâmicas do apêndice A, temos:
Com esse valor, podemos encontrar o trabalho específico exigido pela bomba 1 e depois encontrar a entalpia no ponto 2, então teremos:
E, aplicando o equilíbrio de energia específica para a bomba 1, temos:
Agora, continuando com as propriedades, temos:
Agora, para encontrar a entalpia no ponto 4, vamos aplicar o equilíbrio de energia para a câmara de mistura, então, teremos:
Nesse caso, como temos regime permanente, a equação acima se torna:
Então, aplicando essa equação para a câmara de mistura, temos:
Substituindo os valores conhecidos, temos:
Agora, com esse valor de entalpia e sabendo que no ponto 4 temos líquido, então, podemos pegar pela entalpia de saturação, recorrendo às tabelas termodinâmicas, teremos:
Com esse valor de volume específico, podemos encontrar o trabalho específico para a bomba 2 através de:
E, com isso, aplicando o equilíbrio de energia específica para a bomba 2, podemos encontrar a entalpia no ponto 5, então, teremos:
Passo 2
Agora, dando continuidade as propriedades no ponto de interesse, temos:
Com o valor da entropia do ponto 8, podemos encontrar o título nesse ponto:
E, com esse título, podemos encontrar a entalpia nesse ponto através de:
Passo 3
Agora, para encontrar a potência líquida produzida pela usina. Precisamos da potência produzida e da potência demandada pelas bombas. Sabemos que a potência produzida será a soma da potência produzida pela turbina e a taxa calor gerado pela unidade de processamento, então, a soma dessas potências pode ser escrita em função da variação das entalpias nos pontos de entrada e saída de cada um desses componentes. Dessa forma, temos:
Substituindo os valores conhecidos, chegamos em:
Agora, a potência exigida pelas bombas será:
Dessa forma, a potência líquida para o sistema será:
Passo 4
Agora, para calcular o fator de utilização da usina, precisamos descobrir a taxa de calor gerado na unidade de processamento e o calor fornecido ao sistema. Dessa forma, aplicando o equilíbrio de energia para a unidade de processamento, temos:
E, da mesma forma, aplicando o equilíbrio para a caldeira, chegamos em:
Dessa forma, o fator de utilização será: