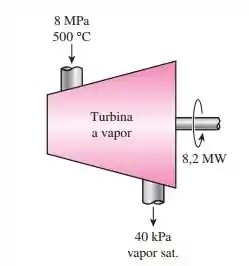
Vapor de água se expande em uma turbina em um processo em regime permanente a uma vazão de 40000 kg/h, entrando a 8 MPa e 500 °C e saindo a 40 kPa como vapor saturado. Considerando que a potência gerada pela turbina é de 8,2 MW, determine a taxa de geração de entropia desse processo. Considere que a vizinhança está a 25 °C.

Para obtermos a geração de entropia, vamos calcular antes a taxa de calor liberada durante o processo:

A equação de balanço de entropia, nesse caso, leva em consideração o sistema formado pela turbina e a vizinhança. Logo,

Assim,