Vapor d'água entra na turbina de uma planta de potência a vapor simples com uma pressão de 10 MPa e uma temperatura T, e se expande adiabaticamente até 6 kPa. A eficiência isentrópica da turbina é de 85%. O líquido saturado sai do condensador a 6 kPa e a eficiência isentrópica
da bomba é 82%.
(a) Determine o título na saída da turbina e a eficiência térmica do ciclo, para T= 580°C.
(b) Construa um gráfico das quantidades do item (a) em função de 7 na faixa de 580 a 700ºC.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
É dado que:
- Pressão na entrada da turbina:
- Pressão do condensador de um ciclo Rankine ideal:
- Eficiência isentrópica da turbina:
- Eficiência isentrópica da bomba:
Passo 3
a) A temperatura na entrada da turbina é igual a
O diagrama de um ciclo Rankine ideal
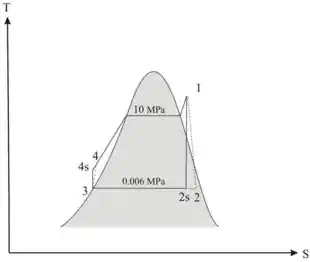
Passo 4
Da tabela de água superaquecida a pressão de e temperatura a entalpia e entropia são
A pressão da tabela de água saturada
Assumindo uma expansão isentrópica, a relação entre as entropias em termos de título
Então, a entalpia no estado 2s é dado por
Passo 5
Já que o processo 1-2 desvia do processo isentrópico a entalpia no estado 2 é dado pela eficiência da turbina
O título vapor correspondente ao vapor na saída da turbina
Passo 6
A entalpia do fluido no estado 3 é dada por
Similarmente, a entalpia do fluido no estado 4s é dada por
Passo 7
Já que o processo 3-4 desvia de um processo isentrópico a entalpia no estado 4 é dado por
Então, a entalpia do fluido em diferentes estados é mostrada na tabela abaixo

Passo 8
O trabalho efetivo feito pelo fluido por ciclo
Similarmente, a taxa de calor transferido para o fluido pelo caldeirão
Passo 9
A eficiência térmica do ciclo é dada por
Passo 10
b) Fazendo a temperatura na entrada da turbina variando de à
Podemos utilizar o software Engineering Equation Solver (EES) pra ajudar a gente a gerar os gráficos
Escrevendo o código no programa:
"Dados Iniciais"
p1 = 100 [bar]
"T1 = 580 [K] vapor saturado"
p2 = 0,06 [bar]
"Turbina"
h1 = Enthalpy (Steam; P = p1; T = T1)
s1 = Entropy (Steam; P = p1; T = T1)
s2s = s1
h2s = Enthalpy (Steam; P = p2; s = s2s)
h2 = Enthalpy (Steam; P = p2; x = x2)
(h1 - h2s) * 0,85 = x2 * (h1 - h2)
Wt = h1 - h2
"Condensador"
p3 = p2
x3 = 0
h3 = Enthalpy (Steam; P = p3; x = x3)
Qsai = h2 - h3
"Bomba"
Wp = h4 - h3
p4 = p1
v3 = Volume (Steam; P = p3; x = x3)
h4s = (h3 + (v3 * (p4 - p3) * 100))
h4s - h3 = (h4 - h3) * 0,82
"Calculos"
Qent = h1 - h4 "adição de calor no gerador de vapor"
Wciclo = Wt - Wp "potência total"
eta = (Wciclo / Qent) * 100 "eficiência térmica"
Passo 11
Colocando os resultados em uma tabela, temos
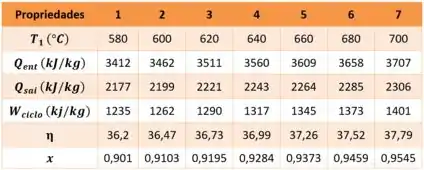
Passo 12
Plotando os gráficos entre várias propriedades com respeito a temperatura de operação
A variação do título
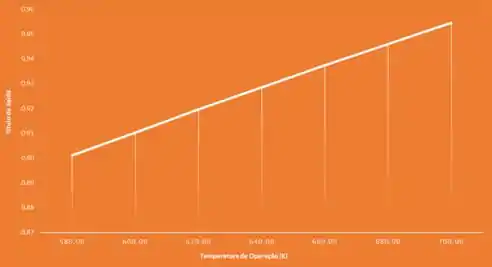
Devido ao aumento da temperatura de operação, o ciclo vai para o diagrama; então, o título da saída do vapor também aumenta no estado 2
Similarmente, para a variação de eficiência do ciclo
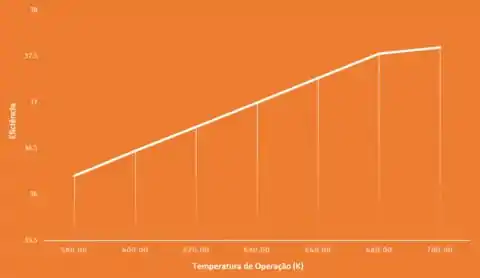
Resposta
a)