Uma planta de potência nuclear baseada no ciclo de Rankine opera com um reator de aquecimento de água para desenvolver uma potência líquida de ciclo de 3 MW. Vapor d’água é ejetado do núcleo do reator a 100 bar e 520°C e expande através de uma turbina até a pressão do condensador, de 1 bar. Líquido saturado sai do condensador e é bombeado até a pressão do reator, de 100 bar. As eficiências isentrópicas da turbina e da bomba são 81% e 78%, respectivamente. A água de resfriamento é admitida no condensador a 15°C com uma vazão mássica de 114,79 kg/s. Determine:
(a) a eficiência térmica.
(b) a temperatura da água de resfriamento ao sair do condensador, em °C.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
a) Desenhando o diagrama para a planta de potência Nuclear no ciclo de Rankine
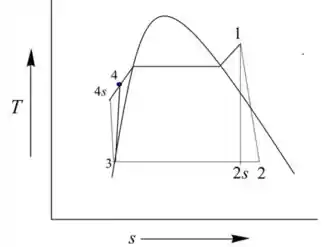
Passo 3
Estado 1
Pegando as propriedades da água a pressão de , temperatura de da Tabela A-4 “Propriedades de Vapor de Água Superaquecido”
Já que o processo 1-2s é isentrópico
Estado 2s
Pegando as propriedades da água a pressão de e entropia de da Tabela A-3 “Propriedades de Água Saturada (Líquido – Vapor): Tabela de Pressão”
Calculando a entalpia no estado 2s
Passo 4
Calculando a entalpia atual no estado 2 usando a eficiência isentrópica da turbina
Obtendo as propriedades no estado 3 da tabela “Propriedades de Água Saturada (Líquido-Vapor): Tabela de Pressão” a
Passo 5
Calculando o trabalho na bomba
Passo 6
Calculando a entalpia no estado 4
Calculando o trabalho na saída da turbina
Calculando a taxa de vazão mássica de vapor
Passo 7
Calculando a eficiência térmica do ciclo
Passo 8
b) Equacionando a taxa de rejeição de calor no condensador para a taxa de calor absorvido pelo refrigerador de água