Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 11.Problemas - Ex. 133
A vazão de refrigerante , num ciclo real de refrigeração, é . O vapor entra no compressor a e e sai dele a e . A potência consumida no compressor foi medida, obtendo-se o valor de . O fluido refrigerante entra válvula de expansão a e e sai do evaporador a e . Nestas condições, determine a taxa de geração de entropia no processo de compressão, a capacidade de refrigeração e o coeficiente de desempenho deste ciclo.
Passo 1
FALA GALERA, salve, salve, firmeza, firmeza (bossa nova tocando no fundo, porque o responde aí também é cultura). Começaremos analisando o diagrama do ciclo real de refrigeração abaixo:
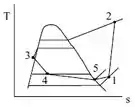
Analisando os estados do diagrama e consultando a tabela conseguimos os seguintes dados:
Estado (1) - ,: ,
Estado (2) - : ,
Estado (3) - ,
Estado (5) - ,:
Estabelecido os dados que serão utilizados, dá uma olhada nas equações que usaremos:
(1)
(2)
(3)
(4)
(5)
(6)
Bem, com tudo isto estabelecido, nós agora podemos ir para o problema!
Passo 2
Primeiramente, começaremos utilizando a equação (1) para descobrir o trabalho do compressor:
Agora, iremos para a equação (2) e calcular a taxa de transição de calor do compressor:
Com esse valor podemos calcular a taxa de geração de entropia com a equação (3):
Feito isto, agora vamos calcular a taxa de transferência de calor no evaporador com a equação (4):
Com isso, utilizaremos a equação (5) para determinar a capacidade de refrigeração:
Por ultimo, utilizaremos a equação (6) para obtermos o coeficiente de desempenho do ciclo:
E dessa forma, me despeço, questão feita com sucesso! Até a próxima pessoal, Love u all!