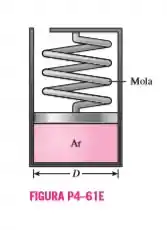
Um volume de 1 p de ar está contido em um dispositivo pistão-cilindro com mola, como mostra a Fig. P461E. A constante da mola é 5 lbf/pol e o diâmetro do pistão é 10 pol. Quando nenhuma força é exercida pela mola sobre o pistão, o estado do ar é 250 psia e 460 °F. Esse dispositivo é então resfriado até que o volume seja metade do volume inicial. Determine a variação na energia interna específica e a entalpia do ar.

Inicialmente, vamos descobrir qual a massa de ar presente dentro do pistão, assim, consideraremos o ar como um gás ideal, logo:

Com a massa do ar, conseguiremos calcular o volume específico do ar no final do processo, temos:

Temos que, conforme o volume vai diminuindo, o tamanho da mola vai aumentando, esse aumento pode ser dado por:

Com isso, conseguiremos encontrar a pressão final do sistema por meio da seguinte expressão:

Utilizando novamente a expressão de um gás ideal, teremos que a temperatura final do processo é dada por:

Agora, para descobrirmos a entalpia e energia interna específica, vamos utilizar os calores específicos, assim: