Determinantes
Teoria
Fala aíííííí! Vamos começar os nossos estudos sobre os determinantes. Animados?!
Antes da gente aprender a calcular deixa eu te dar uma ideia do que são esses tais determinantes.
Quando a gente tem uma matriz, por exemplo, essa aqui de baixo:
A gente pode fazer algumas manipulações com esses números que estão na nossa matriz e obter um único número. Bem, o determinante é isso, vamos fazer alguma manipulação em específico (não é qualquer uma) com esses números que estão na nossa matriz e calcular um único número. Podemos até dizer que esse número serve para caracterizar a nossa matriz, é como se fosse um documento de identificação da nossa matriz.
Ele tem essa carinha daqui
Pegou a ideia? Agora vamos ver aqui como que a gente calcula esses determinantes. Só um aviso, existem várias maneiras de se calcular determinantes de matrizes. Aqui eu vou mostrar as técnicas que funcionam para as matrizes e . Para matrizes maiores, vamos usar outras técnicas, ok?
Vamos lá!
Determinantes de matrizes
Vamos ver aqui como calculamos determinantes de matrizes com 2 linhas e 2 colunas. A regrinha que a gente usa é chamada de regra de Sarrus. Vamos aprender essa regrinha já aplicando para calcular o determinante da seguinte matriz
Para usarmos a regra de Sarrus nas matrizes deste tipo, temos que primeiro calcular o produto dos elementos da diagonal principal, ou seja, esses elementos dessa diagonal aqui:
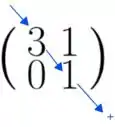
Em que esse sinalzinho de mais nos fala que a gente não muda o sinal. Na nossa matriz, esse produto vai ser:
Guarda esse valor.
Para continuar, temos que calcular o produto dos elementos da diagonal secundária, ou seja, os elementos dessa diagonal aqui:

Em que eu botei aquele sinalzinho de menos para lembrar que nesse produto temos que trocar o sinal. Fazendo este produto, sem esquecer de por um sinal de menos na frente de tudo, temos
Beleza! Só para lembrar, o produto da diagonal principal deu e o produto da diagonal secundária deu . Que que a gente faz com eles?
A regra de Sarrus diz que o determinante da matriz vai ser a soma destes dois resultados:
Viu como é bem direto? Uma dica: Desenhar essas flechinhas que eu desenhei, com o sinal de + na flecha que aponta para baixo e o sinal de – na flecha que aponta para cima ajuda bastante!
Determinantes de Matrizes
Para as matrizes com 3 linhas e 3 colunas, usamos a regra de Sarrus também! Ebaaa! Mas calma, tem uma coisa a mais vamos aprender isso juntos.Vamos calcular o determinante da matriz a seguir:
Nestas matrizes, aquela dica de desenhar umas flechinhas na diagonal vai nos ajudar, mas antes de fazermos isso, vamos precisar fazer uma manipulação na nossa matriz.
A gente repete as duas colunas no final da nossa matriz. Dessa maneira aqui:
Agora sim a gente traça as flechas. As flechas para baixo a gente marca assim:
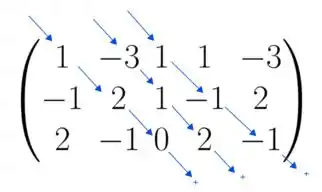
Vamos entender melhor o que a gente vai ter que calcular aqui. Bom, a gente vai ter que calcular o produto de todos os elementos em cada uma das diagonais e depois somar tudo. Só vamos lembrar que nas flechas para baixo a gente não troca o sinal de ninguém, hein.
Vamos lá, na primeira diagonal que eu marquei nós temos os números e o , certo? Nós temos que calcular o produto entre eles:
Deu zero! Tudo bem, vamos para a segunda diagonal. Na segunda diagonal nós temos os números e o 2. O produto entre eles é
Guarda esse aí!
Na última diagonal, temos os números e o . O produto entre eles fica
Lembrando que o produto de dois números negativos é positivo, temos
Agora a gente tem que somar os 3 resultados para as três diagonais:
Opa!! Esse é o resultado das diagonais para baixo, guarda muito bem guardado esse número pois ele vai aparecer na regra de Sarrus!
Muito bem, agora vejamos as flechas para cima:
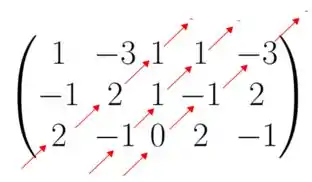
Com essas flechinhas para cima, aquele sinal de menos nos lembra que temos que trocar o sinal dos produtos! Vamos calcular termo a termo aqui para aprendermos.
Na primeira diagonal, nós temos os números e o 1. O produto entre eles é
Beleza? Não! Não esquece de trocar o sinal do produto, o resultado para essa diagonal é
Na segunda diagonal nós temos os números e o . O produto entre eles já com o sinal de menos na frente de tudo fica:
Como menos com menos dá mais, o resultado do produtos dos elementos dessa diagonal é:
Para a terceirda diagonal, temos os números e . Com isso, o produto entre eles, com o sinal trocado é
Agora a gente soma esses três resultados:
Prontinho, usando as flechas para cima, obtemos . Para finalizar o determinante, a regra de Sarrus nos fala que o determinante da matriz vai ser o resultado que a gente obteve usando as flechas para baixo mais o resultado que a gente obteve usando as flechas para cima:
Desta forma, obtemos o determinante das matrizes . Oba!!!
Chegamos ao fim deste tópico ☹
Para você ficar fera em calcular esses determinantes a gente vai ter que praticar um pouco mais. Vamos fazer alguns exercícios?
Te vejo lá!!!! 😊
Determinantes de Matrizes 3 × 3
Exercícios Resolvidos
Exercício Resolvido #1
Geometria Analitica e Algebra Linear – Atividade Teleaula – UNIP
O determinante de é igual a:
Passo 1
Faaaaaaaala ai! Vamos fazer um exercício sobre determinante!!
A gente tem essa matriz aqui:
Podemos usar a regra de Sarrus!
Se você não lembra como ela é, se liga aqui:Para matrizes 2x2, temos que:
Passo 2
Shooow de bola, agora que já relembramos como resolvemos isso, vamos sair da teoria e começar a praticar com os números do enunciado!
Fazendo essas continhas, temos que
Ajeitando os sinais, ficamos com
É isso galerinha! Vamos continuar praticando!
Resposta
Exercício Resolvido #2
Elaboração Própria
Calcule o determinante:
Passo 1
Vamos usar a regra de Sarrus para matrizes de ordem que é a seguinte:
Então, para a matriz do enunciado a gente faz:
Passo 2
Agora é só lembrar que a Relação Fundamental da Trigonometria nos diz que:
Assim, o determinante pedido dá , independente do valor de .
Resposta
Exercício Resolvido #3
Elaboração própria
Considere a matriz
Encontre o valor de para que o valor do determinante de seja
Passo 1
Faaala aí galerinha! Vamos fazer mais uma questão de determinantes!
Bom o nosso enunciado nos dá uma matriz cujo determinante vale ! E temos que achar o valor de , um elemento da matriz!
Temos que
Passo 2
Vamos começar relembrando como a gente calcula o determinante de uma matriz
Para nossa matriz do enunciado, temos que
Passo 3
E o enunciado diz pra gente que
Então é só igualar os dois valores do determinante para achar
Passando o para o outro lado e trocando o sinal dele, ficamos com
Resposta
Exercício Resolvido #4
Lista 1 – Matrizes e Determinantes – UVA
Calcule o determinante a seguir, utilizando a regra de Sarrus
Passo 1
Opa, tudo certinho? Bora pra mais uma questão sobre determinantes!
Temos que a nossa matriz é essa daqui!
O enunciado já diz pra gente usar a regra de Sarrus! Vamos lá
Passo 2
Para usar a regra de Sarrus nas matrizes , temos que repetir as primeiras duas colunas da esquerda da nossa matriz
Passo 3
Segundo, vamos traçar linhas na diagonal principal e nas duas diagonais seguintes
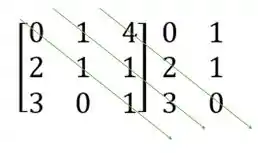
Multiplicar os números que estão na mesma seta e atribuir a eles o sinal de mais
Ajeitando isso, temos que
Passo 4
Depos vamos fazer a mesma coisa com a diagonal secundária e as duas seguintes
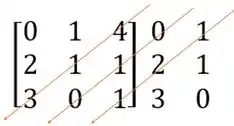
Multiplicando os números que estão na mesma seta e atribuindo a eles o sinal de
Passo 5
Por ultimo é só somar e achar o determinante!
Resposta
Exercício Resolvido #5
Avaliação Algebra Linear I – EE Professora Francisca Pinto Fernandes Rosa
Uma das aplicações que envolvem o cálculo de determinantes de uma matriz de ordem 3 é o cálculo de volume dos vetores escritos na forma matricial. A partir deste cálculo, principalmente na engenharia, podemos projetar a quantidade de material necessário na confecção de peças em geral. Na perspectiva, retomando o processo de cálculo, leia a questão a seguir e assinale a alternativa CORRETA, sendo
Passo 1
Opaaa! Tudo certinho? Vamos pra mais uma questão de determinantes!
Temos que a nossa matriz é essa daqui!
Para acharmos o determinante de uma matriz, 3x3 existem vários métodos. O que vamos usar aqui é o mais famoso, o método de Sarrus!
Passo 2
Primeiro, vamos repetir as primeiras duas colunas da esquerda
Passo 3
Segundo, vamos traçar linhas na diagonal principal e nas duas diagonais seguintes
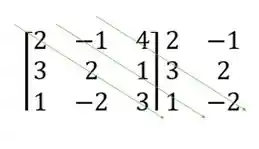
Multiplicar os números que estão na mesma seta e atribuir a eles o sinal de mais
Ajeitando isso, temos que
Passo 4
Depos vamos fazer a mesma coisa com a diagonal secundária e as duas seguintes
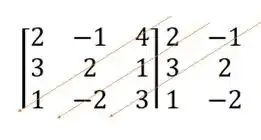
Multiplicando os números que estão na mesma seta e atribuindo a eles o sinal de
Passo 5
Por ultimo é só somar e achar o determinante!
Bora continuar praticando!
Resposta
Exercício Resolvido #6
Elaboração própria
Encontre o valor de na matriz abaixo, sabendo que o determinante
Passo 1
Faala ai galerinha, vamos partir pra cima de mais uma questão de determinantes!
Bom, o enunciado diz pra gente que o determinante vale , ou seja
E ele quer descobrir o valor de
Vamos usar o método de Sarrus! Se liga aqui como a gente vai resolver isso!
Passo 2
Primeiro, vamos repetir as primeiras duas colunas da esquerda
Passo 3
Segundo, vamos traçar linhas na diagonal principal e nas duas diagonais seguintes
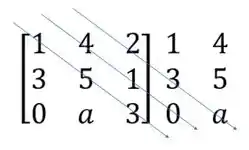
Multiplicar os números que estão na mesma seta e atribuir a eles o sinal de mais
Realizando esses produtos, temos
Passo 4
Depos vamos fazer a mesma coisa com a diagonal secundária e as duas seguintes
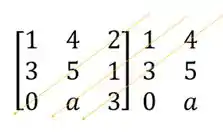
Multiplicando os números que estão na mesma seta e atribuindo a eles o sinal de
Passo 5
Por ultimo é só somar tudo e achar o determinante!
Passo 6
Mas o enunciado diz que
Então, temos que
Resposta
Exercício Resolvido #7
Lista de Exercícios - UTFPR
Calcule o determinante da matriz
Passo 1
Faaala aí!! Vamos seguir com nossos exercícios de determinantes! Essa matéria é muita prática para ficar fera!
Temos que a nossa matriz é essa daqui!
Vamos usar o método de Sarrus!
Passo 2
Primeiro, vamos repetir as primeiras duas colunas da esquerda
Passo 3
Segundo, vamos traçar linhas na diagonal principal e nas duas diagonais seguintes
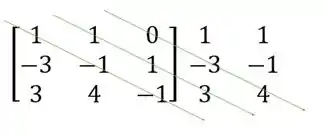
Multiplicar os números que estão na mesma seta e atribuir a eles o sinal de mais
Ajeitando isso, temos que
Passo 4
Depos vamos fazer a mesma coisa com a diagonal secundária e as duas seguintes
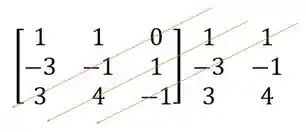
Multiplicando os números que estão na mesma seta e atribuindo a eles o sinal de
Passo 5
Por ultimo é só somar e achar o determinante!
Bora continuar praticando!
Resposta
Exercício Resolvido #8
Lista 1 – Matrizes e Determinantes – UVA
Encontre a solução da equação
Passo 1
Faaaaaala aí! Preparados para mais uma questão de determinantes? Vamos lá!O enunciado dá pra gente o valor do determinante da matriz, que vamos chamar de
E temos que a matriz é essa daqui!
Para calcularmos o determinante, vamos utilizar o método de Sarrus.
Passo 2
Primeiro, vamos repetir as primeiras duas colunas da esquerda
Passo 3
Segundo, vamos traçar linhas na diagonal principal e nas duas diagonais seguintes
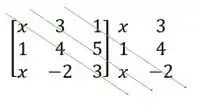
Multiplicar os números que estão na mesma seta e atribuir a eles o sinal de mais
Ajeitando isso, temos que
Passo 4
Depos vamos fazer a mesma coisa com a diagonal secundária e as duas seguintes
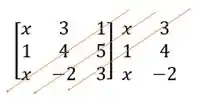
Multiplicando os números que estão na mesma seta e atribuindo a eles o sinal de
Passo 5
Por ultimo é só somar e achar o determinante!
Passo 6
Como o enunciado diz pra gente que o , temos que
Passando o que está multiplicando, dividindo, ficamos com
Resposta
Exercício Resolvido #9
Geometria Analítica – Estacio EAD
Calcule o valor de , a fim de que o determinante da matriz seja nulo
Passo 1
Faaaaala aí, beleza? Vamo que vamo para cima de mais um determinante!
Temos que a nossa matriz é essa daqui!
Para acharmos o determinante de uma matriz, 3x3 existem vários métodos. O que vamos usar aqui é o mais famoso, o método de Sarrus!
Passo 2
Primeiro, vamos repetir as primeiras duas colunas da esquerda
Passo 3
Segundo, vamos traçar linhas na diagonal principal e nas duas diagonais seguintes
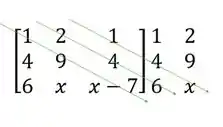
Multiplicar os números que estão na mesma seta e atribuir a eles o sinal de mais
Ajeitando isso, temos que
Passo 4
Depos vamos fazer a mesma coisa com a diagonal secundária e as duas seguintes
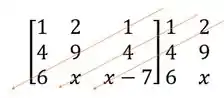
Multiplicando os números que estão na mesma seta e atribuindo a eles o sinal de
Passo 5
Por ultimo é só somar e achar o determinante!
Passo 6
Como o enunciado diz pra gente que o , temos que
Resposta
b)
Exercício Resolvido #10
Lista 1 – Matrizes e Determinantes – UVA
Dadas as matrizes e , calcular o determinante da matriz onde
Passo 1
Faaala galerinha! Vamo que vamo pra mais uma questãozinha de determinantes! Ihuuu
Bom a questão pede o determinante da matriz que é o produto das matrizes e dadas no enunciado
“Putsss mas eu não lembro como fazer multiplicação de matrizes” Não precisa se preocupar! Porque a gente tem uma propriedade de determinante que diz:“O determinante do produto é o produto dos determinantes”
Então só precisamos calcular os determinantes das matrizes e
E só relembrando aqui, quando temos uma matriz , utilizamos essa regrinha aqui para calcular o determinante:
Passo 2
Vamos começar calculando o determinante da matriz
Fazendo as multiplicações, temos:
Então
Passo 3
Agora para a matriz , temos
Fazendo as multiplicações, temos:
Então
Passo 4
Agora é só fazer o produto dos valores que achamos:
Substituindo, temos