Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Propriedades dos Determinantes

Ver Todos os Exercícios

Teoria

Fala aí!

Vamos ver agora umas propriedades de determinantes que vão simplificar a nossa vida.

  1. Determinantes de Matrizes Elementares

    2. Bem, o primeiro passo que devemos tomar quando precisamos calcular algum determinante de alguma matriz é avaliar se a matriz em questão possui algo de especial. Caso a matriz seja ou uma matriz diagonal, triangular superior ou triangular inferior a gente não precisa usar a regra de Sarrus ou o teorema de Laplace ou qualquer outro método. A gente só precisa calcular o produto dos elementos na diagonal principal.

    Não entendeu? Não tem problema, vamos ver na prática como fazemos isso aí.

    Por exemplo, vamos ver como gente calcular o determinante da seguinte matriz:

    A = 11 0 0 0 - 2 0 0 0 3

    Seu dedo deve estar coçando para aplicar a regra de Sarrus já que você se deparou com uma matriz 3 × 3 né? Mas calma lá!

    A matriz A é uma matriz quadrada que possui elementos diferente de zero apenas em sua diagonal principal... Opa!! É uma matriz diagonal então, né?

    Como eu falei lá em cima, para esse tipo de matriz, o determinante aqui é dado pelo produtos dos elementos que estão na diagonal principal. São eles: 11 ,   - 2 e o 3 . Então, podemos escrever:

    det ⁡ A = 11 × - 2 × 3 det ⁡ A =   - 66  

    Viu como é bem direto? Pode confiar, esse método vale sempre que você se deparar com uma das matrizes especiais que eu falei ali em cima.

    Vamos calcular o determinante dessa matriz aqui:

    B = - 1 4 0 0 0 2 0 0 14 3 1 2 5 0 2 7 6

    Arrepiou aí? Aqui também... que matriz monstruosa!

    Mas, olhando bem, ela tem algo de especial. Olha lá, ela é uma matriz quadrada ( 4 × 4 ) e ela só possui elementos diferentes de zero na diagonal e acima da diagonal... Pera aí, essa matriz é uma triangular superior!

    Como eu falei antes, o determinante desse tipo de matriz é obtido calculando o produto entre os elementos da diagonal principal. São eles: - 1 ,   2 ,   5 e o 6 . Então, a gente pode escrever det ⁡ B = - 1 × 2 × 5 × 6 =   - 60

    Bem direto né? Vamos ver mais um exemplo.

    Como vocês calculariam o determinante dessa matriz daqui:

    C = 5 0 2 11 6 2 7 13 0 0 0 5 0 0 0 6

    Essa daqui é uma matriz quadrada ( 4 × 4 ) que só possui elementos diferentes de zero na diagonal e abaixo da diagonal... Pera aí, essa matriz é uma triangular inferior!

    Como eu falei antes, o determinante desse tipo de matriz é obtido calculando o produto entre os elementos da diagonal principal. São eles: 5 ,   2 ,   5 e o 6 . Então, a gente pode escrever det ⁡ C = 5 × 2 × 5 × 6 =   300

    Sim, é só isso mesmo. Sem Sarrus, sem Laplace... então já sabe, a primeira coisa que devemos fazer para calcular qualquer determinante é ver se a matriz em questão é uma dessas matrizes especiais!

  2. Determinantes iguais a zero

    3. Além disso, apenas de olhar uma matriz também já conseguimos ver se o determinante dela vai ser nulo ou não! São três casos para isso, vamos vê-los!

  3. 1° Caso -Determinantes de Matrizes Elementares: Linhas ou Colunas nulas

    4. Se uma linha ou coluna de uma matriz for completamente nula, como essa:

    Então podemos dizer que o determinante é igual a zero!

    det ⁡ A = 0

  4. 2° Caso -Determinantes de Matrizes Elementares: Linha ou coluna iguais a outras linhas ou colunas

    5. Vamos supor agora que tenhamos essa matriz aqui:

    A = 1 7 0 6 4 9 0 2 1 7 0 6

    Nós percebemos que a primeira linha e a terceira linha são iguais, certo?!

    Como elas são iguais, também podemos afirmar que o determinante da matriz é igual a zero!

    det ⁡ A = 0

  5. 3° Caso -Determinantes de Matrizes Elementares: Linha ou coluna múltiplas de outras linhas ou colunas

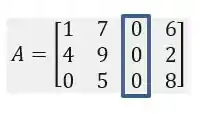
    6. Esse último caso ocorre quando temos uma linha ou coluna que é múltipla de outra linha ou coluna, veja:

    B = 1 2 1 6 4 8 5 2 1 2 10 6

    Vamos olhar com atenção para a matriz B ! Veja que a coluna 2 é o dobro da coluna 1, ou seja, todos os números da coluna 2 são iguais se multiplicarmos os valores da coluna 1 por 2:

    B = 1 1 × 2 = 2 1 6 4 4 × 2 = 8 5 2 1 1 × 2 = 2 10 6

    Nesse caso também podemos afirmar que o determinante será igual a zero! Ou seja, sempre que tivermos um número multiplicando toda uma linha ou coluna para gerar outra linha ou coluna, vamos dizer que o determinante é nulo:

    det ⁡ B = 0

  6. Determinantes multiplicados

    7. O determinante original de uma matriz será multiplicado por um número em dois casos que vamos ver agora!

  7. 1° Caso -Determinantes multiplicados: Linha ou coluna multiplicado por um número

    8. Caso uma linha ou coluna por um número qualquer, podemos multiplicar o determinante pelo mesmo número, por exemplo, temos inicialmente a seguinte matriz com o seu determinante:

    C = 1 2 3 9 → det ⁡ C = 3

    Se nós multiplicarmos a primeira linha por 2, então temos a seguinte matriz:

    C ' = 2 × 1 2 × 2 3 9 = 2 4 3 9

    O novo determinante será igual a:

    det ⁡ C ' = 18 - 12 = 6

    Que é exatamente o mesmo número 2 que multiplicou a primeira linha, que nesse momento multiplica o determinante:

    det ⁡ C ' = 6 = 2 × 3 = 2 × d e t ⁡ ( C )

  8. 2° Caso -Determinantes multiplicados: Matriz quadrada multiplicada por um número

    9. Caso uma matriz quadada de dimensão n × n seja multiplicada por um número k , então o determinante original será multiplicado pelo mesmo k elevado pelo n da dimensão da matriz. Pareceu confuso? Calma que eu vou dar um exemplo tranquilo!

    Olha pra essa matriz quadrada 3 × 3 e seu determinante é igual a:

    D = 1 2 1 3 1 2 2 3 1 → det ⁡ D = 4

    Se multiplicarmos a matriz D pelo número 2 , então chegamos na matriz D ' :

    D ' = 2 × D = 2 × 1 2 1 3 1 2 2 3 1 = 2 × 1 2 × 2 2 × 1 2 × 3 2 × 1 2 × 2 2 × 2 2 × 3 2 × 1

    Após multiplicarmos todos os elementos pelo mesmo número 2 , encontramos a seguinte matriz que tem o determinante:

    D ' = 2 4 2 6 2 4 4 6 2 → det ⁡ D ' = 32

    Mas vamos comparar esse determinante com o original? Se nós multiplicarmos o determinante original:

    det ⁡ D = 4

    Pelo número 2 que foi usado para multiplicar a matriz D , quando elevado pelo número de linhas e colunas da matriz D , ou seja, o número 2 elevado a 3 :

    2 3 = 2 × 2 × 2 = 8

    Então teremos:

    det ⁡ D ' = 2 3 × det ⁡ D = 2 3 × 4 = 8 × 4 = 32

    Mas pra que isso serve? Bom, se você já tivesse calculado o determinante da matriz original D e a outra questão pedisse o determinante de uma matriz que é múltipla de D então você poderia simplificar seu cálculo, apenas multiplicando seu determinante original por um número elevado a outro!

  10. Oposto do determinante

    11. Olha, você pode imaginar o que acontece com o determinante de uma matriz se você já tiver calculado ele e depois trocar duas linhas de lugar? Bom, eu vou te mostrar, vamos pensar nessa matriz aqui:

    E = 1 2 1 3 1 2 2 3 1 → det ⁡ E = 4

    Supondo que vamos trocar a primeira linha com a terceira linha, então nossa nova matriz será a seguinte:

    E ' = 2 3 1 3 1 2 1 2 1

    Se nós calcularmos esse determinante novamente, chegaremos em:

    det ⁡ E ' = 2 3 1 2 3 3 1 2 3 1 1 2 1 1 2

    det ⁡ E ' = 2 3 1 2 3 3 1 2 3 1 1 2 1 1 2

    det ⁡ E ' = 2 × 1 × 1 + 3 × 2 × 1 + 1 × 3 × 2 - [ 3 × 3 × 1 + 2 × 2 × 2 + ( 1 × 1 × 1 ) ]

    det ⁡ E ' = 2 + 6 + 6 - 9 + 8 + 1 = 14 - 18 = - 4

    Ou seja, apenas ao invertermos as linhas da matriz E de lugar para conseguirmos a nova matriz E ' , nós percebemos que o determinante de E ' é o oposto do determinante de E !

    det ⁡ E = 4 → det ⁡ E ' = - 4

  11. Teorema de Binet

Se duas matrizes A e B forem quadradas e da mesma dimensão, então podemos encontrar o determinante da matriz resultante do produto entre A e B a partir dos determinantes de A e B :

det ⁡ A ⋅ B = det ⁡ A ⋅ d e t ⁡ ( B )

Vamos ver um exemplo simples, certo? Veja as duas matrizes quadradas de mesmas dimensões 2 × 2 :

A = 1 2 3 4

B = 3 7 5 6

Vamos calcular o determinante de A :

det ⁡ A = 1 × 4 - 2 × 3 = 4 - 6 = - 2

Fazemos o mesmo para a matriz B :

det ⁡ B = 3 × 6 - 7 × 5 = 18 - 35 = - 17

Multiplicando esses dois determinantes, o que nós encontraremos?

det ⁡ A ⋅ det ⁡ B = - 2 ⋅ - 17 = + 34

A multiplicação de dois números negativos resulta em um número positivo!

Agora vamos fazer o produto entre as matrizes A e B :

A ⋅ B = 1 2 3 4 ⋅ 3 7 5 6 = 3 ⋅ 1 + 5 ⋅ 2 7 ⋅ 1 + 6 ⋅ 2 3 ⋅ 3 + 5 ⋅ 4 7 ⋅ 3 + 6 ⋅ 4 = 13 19 29 45

Qual é o determinante dessa nova matriz?

det ⁡ A ⋅ B = 13 ⋅ 45 - 19 ⋅ 29 = + 34

Assim:

det ⁡ A ⋅ B = det ⁡ A ⋅ det ⁡ B = 34

Belezinha?? Vamos treinar para ficarmos feras resolvendo esses determinantes!

Te vejo nos exercícios 😊

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Classifique as matrizes abaixo em diagonal, triangular superior e triangular inferior:

A = 3 0 0 5 5 0 2 7 9

B = 6 0 0 0 54 0 0 0 29

C = 13 43 21 0 5 78 0 0 94

D = 1 0 3 2

Passo 1

Primeira coisa que a gente tem que olhar nesses exercícios, é se a matriz é quadrada... não lembra o que é isso? Tudo bem... é só ver se o número de linhas é igual ao número de colunas! Por quê temos que ver isso? É que as matrizes diagonal, triangular superior e triangular inferior são todas quadradas!!

Só de olhar as matrizes do nosso problema, vemos que todas são quadradas... UFA!

Analisando a primeira matriz A , o primeiro passo que fazemos é olhar para a diagonal principal:

A = 3 0 0 5 5 0 2 7 9

Percebemos que todos os elementos acima da diagonal principal são iguais a zero, enquanto todos os elementos abaixo da diagonal principal são diferentes de zero.

Isso significa que se trata de uma matriz triangular inferior.

Passo 2

Agora, passando para a análise da matriz B , temos a diagonal principal:

B = 6 0 0 0 54 0 0 0 29

Percebemos que todos os elementos acima e abaixo da diagonal principal são iguais a zero, então a matriz B é uma matriz diagonal.

Passo 3

Analisando a matriz C , temos:

C = 13 43 21 0 5 78 0 0 94

Vemos que acima da diagonal principal, temos todos os elementos diferentes de zero, diferente dos elementos abaixo da diagonal principal. Assim, a matriz C é uma matriz triangular superior.

Passo 4

Vamos dar uma olhadinha na matriz D.

Todas as matrizes que vimos antes eram 3 × 3 , mas a matriz D é 2 × 2 :

D = 1 0 3 2

Mas eu quero mostrar que a análise será a mesma com matrizes grandes e pequenas, vamos sempre começar olhando para a diagonal principal:

D = 1 0 3 2

Abaixo da diagonal principal, temos o número 3 e acima da diagonal principal, temos o número 0 . Dessa forma é uma matriz triangular inferior.

Resposta

A = 3 0 0 5 5 0 2 7 9 : Matriz triangular inferior

B = 6 0 0 0 54 0 0 0 29 : Matriz diagonal

C = 13 43 21 0 5 78 0 0 94 : Matriz triangular superior

D = 1 0 3 2 : Matriz triangular inferior

Exercício Resolvido #2

[ESTÁCIO – Álgebra Linear]

Considere a matriz A , n × n . Se duas linhas (ou colunas) de A forem proporcionais, então, o determinante da matriz A é

Passo 1

Primeira coisa, o que quer dizer “proporcional”?

Quer dizer que dois objetos são relacionados pela multiplicação de um número.

Por exemplo, olhe para essa matriz 2 × 2 :

1 2 1 2

Concorda que se eu multiplicar toda a primeira coluna:

1 1

Pelo número 2 , eu encontro a segunda coluna? Veja:

1 ⋅ 2 = 2 1 ⋅ 2 = 2

Encontramos a segunda coluna:

2 2

Passo 2

Mas temos uma regra clara para determinante, sabe qual é? Qualquer matriz que uma linha ou coluna seja múltipla de outra linha ou coluna, ou seja, linhas ou colunas proporcionais, o determinante é ZERO!

Chocante? Eu acho que não dá pra esquecer mais!

Então não fica com medo, essa matriz A tem determinante igual a zero!

Resposta

Zero

Exercício Resolvido #3

Elaboração própria

Calcule o determinante da matriz abaixo:

A = 1 2 5 2 4 7 3 6 9

Passo 1

Primeiro passo para um determinante é sempre olhar a relação entre as linhas e as colunas. Pois caso alguma linha seja múltipla de outra linha, ou uma coluna seja múltipla de outra coluna, o determinante será igual a zero.

Passo 2

Olhe para a primeira e a segunda linha:

1 2 5 2 4 7

Olhando de início, parece que a segunda linha é o dobro da primeira, o dobro da primeira linha seria:

1 ⋅ 2 = 2 2 ⋅ 2 = 4 5 ⋅ 2 = 10

Os números que são diferentes são o 5 e 7. Então uma linha não é o múltiplo da outra.

Certo, ainda podemos ter um determinante!

Passo 3

Continuando, vamos olhar a relação entre a primeira coluna e a segunda coluna:

1 2 2 4 3 6

Percebe que se multiplicarmos a primeira coluna por 2 , encontraremos o valor da segunda coluna? Veja:

1 ⋅ 2 = 2 2 ⋅ 2 = 4 3 ⋅ 2 = 6

Ou seja, uma coluna é múltipla da outra! Logo o determinante será igual a zero!

Deixando claro uma coisa, pessoal, caso não fosse múltiplos, continuaríamos investigando a relação entre a coluna 1 com a 3, entre a 2 e a 3. Caso todas não fossem múltiplas entre si, ai sim poderíamos começar a fazer o determinante!

Resposta

Zero

Exercício Resolvido #4

[ESTÁCIO – Álgebra Linear]

A matemática é repleta de regras e fórmulas, e cada uma foi criada visando a facilitar a vida do ser humano. Os estudos sobre a matriz vêm desde o século X I X e trazem uma nova experiência ao campo da matemática. Sobre as matrizes e os elementos associados, classifique V para as sentenças verdadeiras e F para as falsas:

( ) O determinante de uma matriz triangular superior é dado pela multiplicação dos termos da diagonal principal.

( ) Ao permutar duas linhas de uma matriz, o determinante dessa matriz não muda de sinal.

( ) O determinante de uma matriz com duas linhas ou colunas iguais é zero.

( ) Se todos os elementos de uma linha ou de uma coluna de uma matriz forem iguais a 1, então o determinante dessa matriz será igual a zero.

Assinale a alternativa que apresenta a sequência CORRETA:

  1. V - F - V - F
  2. F - V - F - V
  3. F - V - F - F
  4. V - F - V - F

Passo 1

Analisando a primeira afirmativa:

“O determinante de uma matriz triangular superior é dado pela multiplicação dos termos da diagonal principal.”

Que está corretíssima, veja esse exemplo:

A = 1 2 3 0 4 5 0 0 6

A diagonal principal é:

A = 1 2 3 0 4 5 0 0 6

Abaixo da diagonal principal temos apenas números zero e só temos números na diagonal e acima dela:

A = 1 2 3 0 4 5 0 0 6

Isso significa que essa matriz é triangular superior, logo o determinante da matriz A é a multiplicação entre os elementos da diagonal principal:

det ⁡ A = 1 ⋅ 4 ⋅ 6 = 24

Então a primeira afirmativa é V!

Passo 2

A segunda afirmação:

“Ao permutar duas linhas de uma matriz, o determinante dessa matriz não muda de sinal.”

Vamos olhar um exemplo pra ver se isso se aplica:

A = 1 2 3 4

O determinante é igual a:

det ⁡ A = 1 ⋅ 4 - 2 ⋅ 3 = 4 - 6 = - 2

Caso alteremos as linhas da matriz, vamos encontrar uma nova matriz:

B = 3 4 1 2

O determinante da nova matriz é igual a:

det ⁡ B = 3 ⋅ 2 - 1 ⋅ 4 = 6 - 4 = 2

Ou seja, verificamos com um exemplo que o sinal foi alterado sim! E deixa que eu te adianto que sempre que uma matriz tiver um determinante diferente de zero, então quando trocarmos duas linhas de lugar, iremos alterar o sinal, sim!

Logo a afirmativa é falsa!

Passo 3

Analisando a terceira afirmativa:

“O determinante de uma matriz com duas linhas ou colunas iguais é zero.”

Essa afirmativa está corretíssima! Por exemplo:

A = 1 1 1 1

Calculando o determinante:

det ⁡ A = 1 ⋅ 1 - 1 ⋅ 1 = 1 - 1 = 0

Esse é só um exemplo, mas a regra é ainda mais ampla:

Se alguma linha ou coluna for múltipla de outra linha ou coluna da matriz, o determinante é zero!

Não esquece, beleza?!

Então essa afirmativa é verdadeira!

Passo 4

Agora vamos analisar a última afirmativa:

“Se todos os elementos de uma linha ou de uma coluna de uma matriz forem iguais a 1, então o determinante dessa matriz será igual a zero.”

Vamos ver uma matriz que contradiz completamente essa ideia:

A = 1 0 0 1 2 0 1 3 4

Temos essa coluna feita completamente por 1 :

1 0 0 1 2 0 1 3 4

Ao mesmo tempo, olhe para a diagonal principal:

1 0 0 1 2 0 1 3 4

Abaixo, da diagonal principal, todos os espaços estão preenchidos, enquanto acima da diagonal principal, só temos zeros. Logo, se trata de uma matriz triangular inferior e para matrizes triangulares inferiores, o determinante é igual a multiplicação entre os elementos da diagonal principal.

Então, o determinante dessa matriz é igual a:

det ⁡ A = 1 ⋅ 2 ⋅ 4 = 8

Que é completamente diferente de 0 , ou seja, a afirmação é falsa!

Passo 5

Reunindo todas as análises que fizemos anteriormente:

  1. O determinante de uma matriz triangular superior é dado pela multiplicação dos termos da diagonal principal. VERDADEIRO
  2. Ao permutar duas linhas de uma matriz, o determinante dessa matriz não muda de sinal. FALSO
  3. O determinante de uma matriz com duas linhas ou colunas iguais é zero. VERDADEIRO
  4. Se todos os elementos de uma linha ou de uma coluna de uma matriz forem iguais a 1, então o determinante dessa matriz será igual a zero. FALSO

Logo nossa resposta será a letra “d”!

Resposta

d) V - F - V - F

Exercício Resolvido #5

Elaboração própria

Calcule o determinante da matriz:

A = - 1 0 0 2 3 0 4 - 2 5

Passo 1

Bom pessoal, a primeira coisa que sempre temos que fazer é verificar se a matriz do nosso problema é alguma daquelas matrizes especiais... não lembra? São elas: diagonal, triangular superior, triangular inferior. A gente faz isso dando, primeiro, uma olhada na diagonal principal:

- 1 0 0 2 3 0 4 - 2 5

Percebe comigo que abaixo da diagonal principal, temos todos os elementos diferentes de zero, enquanto acima da diagonal principal, todos os elementos são iguais a zero.

Isso significa que se trata de uma matriz triangular inferior.

Passo 2

Temos uma regra para matrizes triangulares inferiores e superiores, o determinante para essas matrizes é igual a multiplicação entre os elementos da diagonal principal.

Ou seja, no caso da matriz:

A = - 1 0 0 2 3 0 4 - 2 5

O determinante será igual a:

det ⁡ A = - 1 ⋅ 3 ⋅ ( 5 )

Passo 3

Vamos fazer essa multiplicação então:

det ⁡ A = - 1 ⋅ 3 ⋅ ( 5 )

Vamos multiplicar apenas os números, depois pensaremos no sinal, ok? Logo:

1 ⋅ 3 ⋅ 5 = 3 ⋅ 5 = 15

A multiplicação de um número negativo por outro número positivo é igual a um número negativo:

det ⁡ A = - 15

Isso aí! Chegamos na resposta!

Resposta

det ⁡ A = - 15

Exercício Resolvido #6

[ESTÁCIO – Álgebra linear- Modificada]

Dada as matrizes A e B , calcule o valor do determinante de 10 A - B :

A = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 2

B = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 10 0

Passo 1

Pessoal, primeiro de tudo, temos uma multiplicação de um escalar por uma matriz 10 A . Logo, devemos multiplicar cada elemento da matriz por esse escalar:

10 ⋅ A = 10 ⋅ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 2 = 10 ⋅ 1 10 ⋅ 0 10 ⋅ 0 10 ⋅ 0 10 ⋅ 0 10 ⋅ 1 10 ⋅ 0 10 ⋅ 0 10 ⋅ 0 10 ⋅ 0 10 ⋅ 1 10 ⋅ 0 10 ⋅ 0 10 ⋅ 0 10 ⋅ 1 10 ⋅ 2

Qualquer número multiplicado por zero é igual a zero, então:

10 ⋅ A = 10 ⋅ 1 0 0 0 0 10 ⋅ 1 0 0 0 0 10 ⋅ 1 0 0 0 10 ⋅ 1 10 ⋅ 2

Realizando as multiplicações de 10 por 1 e por 2 :

10 ⋅ 1 = 10

10 ⋅ 2 = 20

Substituindo na matriz:

10 ⋅ A = 10 0 0 0 0 10 0 0 0 0 10 0 0 0 10 20

Passo 2

Agora vamos subtrair a matriz 10 A da matriz B :

10 ⋅ A - B = 10 0 0 0 0 10 0 0 0 0 10 0 0 0 10 20 - 0 0 0 0 0 0 0 0 0 0 0 0 0 0 10 0

Vamos realizar a subtração entre os elementos correspondentes a mesma posição na matriz:

10 0 0 0 0 10 0 0 0 0 10 0 0 0 10 20 - 0 0 0 0 0 0 0 0 0 0 0 0 0 0 10 0 = 10 - 0 0 - 0 0 - 0 0 - 0 0 - 0 10 - 0 0 - 0 0 - 0 0 - 0 0 - 0 10 - 0 0 - 0 0 - 0 0 - 0 10 - 10 20 - 0

Temos basicamente quatro subtrações diferentes:

0 - 0 = 0

10 - 0 = 10

20 - 0 = 20

10 - 10 = 0

Substituindo esses valores na nova matriz, ficaremos com:

10 ⋅ A - B = 10 0 0 0 0 10 0 0 0 0 10 0 0 0 0 20

Chegamos então na matriz que temos que descobrir o determinante, vamos para esse passo agora.

Passo 3

Essa matriz ficou grandona né? Mas ela tá suspeita de ser alguma matriz que a gente conhece... Vamos olhar para a diagonal principal:

10 ⋅ A - B = 10 0 0 0 0 10 0 0 0 0 10 0 0 0 0 20

Veja que abaixo da diagonal principal, temos apenas zeros, enquanto acima da diagonal principal, também temos apenas zeros. Isso significa que essa matriz é diagonal!

Mas o que isso impacta o nosso determinante? É simples, temos uma regrinha que diz que o determinante de matrizes de diagonais é igual a produto entre os elementos da diagonal principal, logo:

det ⁡ 10 ⋅ A - B = 10 ⋅ 10 ⋅ 10 ⋅ 20

Essa multiplicação é igual a:

det ⁡ 10 ⋅ A - B = 20.000

Pronto, achamos a resposta. Viu que tudo se resolveu com apenas uma regra? Temos que memorizar e não esquecer mais.

Resposta

det ⁡ 10 ⋅ A - B = 20.000

Exercício Resolvido #7

Elaboração própria

Determine o produto x ⋅ y a partir da matriz A :

A = y 0 0 0 x 0 0 0 4

Dado que o determinante da matriz é 20 .

Passo 1

Quando falamos sobre o determinante de uma matriz, a primeira coisa que fazemos é olhar para a diagonal principal:

A = y 0 0 0 x 0 0 0 4

Percebemos que todos os elementos acima e abaixo da diagonal principal são iguais a zero, então a matriz A é uma matriz diagonal.

Passo 2

Temos uma regra importante: em matrizes diagonais, o determinante é igual ao produto da diagonal principal, logo no caso da matriz A , o determinante é igual a:

y ⋅ x ⋅ 4 = 20

Sendo que o valor 20 foi dado no enunciado.

Passo 3

Essa multiplicação:

y ⋅ x ⋅ 4 = 20

Podemos passar o 4 para o outro lado, deixando apenas as incógnitas do lado esquerdo da igualdade:

y ⋅ x = 20 4

Essa divisão é igual a:

y ⋅ x = 5

Através da propriedade comutativa da multiplicação, podemos trocar os termos x e y de lugar:

y ⋅ x = x ⋅ y = 5

Então encontramos a nossa resposta! Maravilha!

Resposta

x ⋅ y = 5

Exercício Resolvido #8

Elaboração própria

Determine o valor da incógnita x na matriz A :

A = x 9 6 8 0 4 3 2 0 0 2 x 1 0 0 0 5

Dado que o determinante da matriz A é igual a 40 .

Passo 1

Primeira coisa que fazemos é olhar para a diagonal principal:

A = x 9 6 8 0 4 3 2 0 0 2 x 1 0 0 0 5

Percebemos que todos os elementos acima da diagonal principal são diferentes de zero, enquanto todos os elementos abaixo da diagonal principal são iguais a zero. Isso significa que se trata de uma matriz triangular superior.

Passo 2

Temos uma regra sobre o determinante de matrizes triangulares superiores e inferiores, o determinante é igual a multiplicação entre os termos da diagonal principal.

A = x 9 6 8 0 4 3 2 0 0 2 x 1 0 0 0 5

Logo, o determinante da matriz A é:

det ⁡ A = x ⋅ 4 ⋅ 2 x ⋅ 5

Passo 3

O enunciado nos disse que esse determinante é igual a 40 , então vamos igualar essa expressão do determinante a 40 :

det ⁡ A = x ⋅ 4 ⋅ 2 x ⋅ 5 = 40

Para resolver essa equação, vamos multiplicar os elementos:

x ⋅ 4 ⋅ 2 x ⋅ 5 = 40 x ⋅ x

Multiplicamos primeiro todos os coeficientes numéricos, que nada mais são que os números. Agora multiplicando a variável x :

40 x ⋅ x = 40 x 2

Passo 4

Igualando a multiplicação que encontramos:

det ⁡ A = 40 x 2 = 40

Isolando o x de um lado da equação só, vamos passar o 40 para o outro lado dividindo:

x 2 = 40 40

Logo:

x 2 = 1

Quando a gente tem esse tipo de equação que envolve de um lado x 2 e do outro um número, tiramos a raiz quadrada nos dois lados, tomando o cuidado em por ± na frente do número:

x 2 = ± 1

Como a raiz quadrada de 1 é 1 mesmo, temos:

x   =   ± 1

Existem duas possibilidades para a incógnita x :

x = 1 ou x = - 1

Então essa será a nossa resposta!

Resposta

x = 1 ou x = - 1

Exercício Resolvido #9

Elaboração própria

Determine o valor de x e y na matriz A :

A = x 0 0 5 2 0 3 1 y

Dado que a soma dos elementos da primeira coluna é igual a 13 e o determinante da matriz é igual a 30 .

Passo 1

A primeira informação sobre a matriz que o enunciado nos dá, é que a soma dos elementos da primeira coluna é 13 . Os elementos da primeira coluna são:

A = x 0 0 5 2 0 3 1 y

Somando todos os elementos:

x + 5 + 3 = 13

Então vamos isolar o x de um lado só e encontrar o número do outro lado da igualdade:

x = 13 - 5 - 3

Subtraindo esses números, chegamos a:

x = 5

Substituindo na matriz:

A = 5 0 0 5 2 0 3 1 y

Pronto, já achamos a primeira incógnita! Vamos encontrar o valor de y agora.

Passo 2

A segunda informação passada é sobre o determinante da matriz, então o primeiro passo que faremos será olhar para a diagonal principal:

A = 5 0 0 5 2 0 3 1 y

Percebemos que todos os elementos acima da diagonal principal são iguais a zero, enquanto todos os elementos abaixo da diagonal principal são diferentes de zero.

Isso significa que se trata de uma matriz triangular inferior.

Passo 3

Temos uma regra sobre o determinante de matrizes triangulares superiores e inferiores, o determinante é igual a multiplicação entre os termos da diagonal principal.

Logo, o determinante da matriz é:

det ⁡ A = 5 ⋅ 2 ⋅ y = 30

Só precisamos resolver essa igualdade para achar o valor de y . Vamos começar resolvendo aquele produto ali:

5   .   2   .   y   =   10   .   y

Então temos

10   .   y   =   30

Vamos então passar todos os números para um lado só da igualdade e isolar o y :

y = 30 10 = 3

Pronto, encontramos o valor de y

y = 3

Logo, a matriz é

A = 5 0 0 5 2 0 3 1 3

Resposta

x = 5

y = 3

Exercício Resolvido #10

Elaboração própria

Calcule o determinante da matriz D :

D = 2 7 9 5 3 0 8 6 3 1 0 0 9 3 6 0 0 0 1 4 0 0 0 0 2

Passo 1

Calma, eu sei que essa matriz assusta, porque ela é muito grande, mas vamos enfrentar isso juntos e vou te mostrar que é um problema simples de resolver.

Vamos começar analisando a matriz D , o primeiro passo que fazemos é olhar para a diagonal principal:

D = 2 7 9 5 3 0 8 6 3 1 0 0 9 3 6 0 0 0 1 4 0 0 0 0 2

Percebemos que todos os elementos acima da diagonal principal são diferentes de zero, enquanto todos os elementos abaixo da diagonal principal são iguais a zero.

Isso significa que se trata de uma matriz triangular superior.

Passo 2

A regra que já conhecemos é que o determinante de matrizes diagonais, triangulares superiores e triangulares inferiores é dado pelo produto entre os elementos da diagonal principal.

Esse é o nosso caso, então só precisamos nos preocupar com os elementos que eu destaquei aqui:

D = 2 7 9 5 3 0 8 6 3 1 0 0 9 3 6 0 0 0 1 4 0 0 0 0 2

det ⁡ D = 2 ⋅ 8 ⋅ 9 ⋅ 1 ⋅ 2

Fazendo essa multiplicação por partes, multiplicando 2   por 8 :

det ⁡ D = 16 ⋅ 9 ⋅ 1 ⋅ 2

Multiplicando 16 por 9 :

det ⁡ D = 144 ⋅ 1 ⋅ 2

Qualquer número multiplicado por 1 é igual a ele mesmo:

det ⁡ D = 144 ⋅ 2

Agora só resta multiplicar 144 por 2 :

det ⁡ D = 288

Chegamos a resposta final e você viu que é bem simples, independentemente do tamanho da matriz!

Resposta

det ⁡ D = 288