Matrizes Inversas
Teoria
Fala aí!! Aqui vamos aprender quem são essas matrizes inversas, como elas aparecem e vamos entender a ideia por trás delas, belezinha?
Vamos começar lembrando dos números. Vocês já ouviram falar de inversa de um número? Não é estranho esse nome né? Por exemplo, o número , existe um número (vou chamar de “” só para a gente conhecer, mas logo logo a gente vai ver quem é esse núemro) que quando multiplicamos o nosso por esse número, o resultado é 1. Olha só:
Quando isso acontece, a gente diz que o número é a inversa do número . E a gente sabe quem tem que ser o para que isso aconteça. Na nossa expressão de cima a gente pode passar aquele 2 que está multiplicando o no lado esquerdo da igualdade para o lado direito. Quando fazemos isso, ele tem que passar dividindo. Assim, ó:
Como estamos falando de números, a inversa de qualquer número vai ser sempre dividido pelo número!! Uma outra maneira de escrever o , que vai ser bem útil, é a seguinte:
Show?
Você deve estar se perguntando o que que isso tem a ver com as matrizes né? A ideia é exatamente a mesma! Se tivermos uma matriz , sua inversa vai ser uma matriz que a gente chama de tal que se fizermos o produto matricial de por o resultado tem que ser
Onde é a matriz identidade (é como se fosse o número que a gente discutiu quando falamos dos números ali em cima).
Ficou confuso? Tudo bem, vamos esclarecer ponto a ponto com um exemplo.
Vamos aprender aqui a calcular a inversa da seguinte matriz:
Para entendermos melhor essas matrizes inversas, eu vou te dar um spoiler que depois que realizarmos o procedimento para calcular a inversa dessa matriz , a gente vai obter a seguinte matriz inversa:
Por que eu já estou lhe dando a resposta? Para a gente ver o resultado do produto entre e :
Vamos lembrar aqui como que a gente calcula esse produto matricial. Os elementos da matriz resultante de um produto matricial são sempre calculados realizando o produto dos elementos nas linhas de uma matriz com os elementos das colunas da outra matriz.
Vamos fazer isso, começando com a primeira linha de com a primeira coluna de , resultando no elemento da primeira linha e primeira coluna da matriz resultado:
a
Realizando essas operações para as matrizes demais:
Realizando as operações de produto e depois as de soma, temos, por fim:
Opa!! O resultado desse produto da matriz por sua inversa resultou naquela matriz ali que só tem 1 em sua diagonal princial e os elementos restantes são nulos. Essa é exatamente a matriz identidade do tipo , ou .
Pegou a ideia de quem é a matriz inversa e o que ela faz? Agora vamos ao procedimento para calcular a inversa de uma matriz.
Uma última observação: a gente só consegue usar calcular essas inversas de matrizes quadradas (matrizes em que o número de linhas é igual ao número de colunas) e matrizes cujo o determinante é diferente de zero. Caso apareça aguma matriz cujo o determinante é nulo, dizemos que se trata de uma matriz não inversível.
Procedimento para inverter uma matriz
Para realizar o procedimento que eu vou ensinar a vocês a gente precisa, primeiro, escrever a matriz que a gente deseja inverter ao lado da matriz identidade do mesmo tipo que a nossa matriz. Como desejamos inverter a seguinte matriz :
Precisamos escrevê-la ao lado de uma matriz identidade também dessa forma aqui:
Feito isso, já podemos realizar o nosso procedimento. Um detalhe importante é que a gente foca a nossa atenção em mexer na nossa matriz mas tudo que fizermos nela, temos que fazer a mesma operação naquela matriz identidade que está ao lado.
O procedimento de inversão de uma matriz quadrada é o seguinte
- Escalonamos a matriz ;
- Transformamos essa matriz escalonada em uma matriz identidade.
Vamos fazer esse procedimento em nossa matriz. Bom, precisamos escalonar nossa matriz realizando as mesmas operações na matriz identidade ao lado. Mas olha só... Nossa matriz A já está na forma escalonada, pode conferir! Ou seja, o primeiro passo, nesse exemplo, já veio pronto. Vamos para o segundo passo!
Precisamos transformar essa matriz em uma matriz identidade. Como fazemos isso? Vamos aprender isso!
A matriz identidade é uma matriz que possui elementos somente em sua diagonal principal. Se olharmos a nossa matriz ela possui um ali na primeira linha e segunda coluna estragando a nossa festinha ☹ Vamos sumir com ele!! Para elimarmos ele, a gente pode realizar a seguinte operação elementar:
Cuidado hein!! Temos que fazer essa operação nas duas matrizes:
Realizando essas subtrações, temos
Opa!! Nossa matriz já virou uma matriz diagonal! Para continuarmos, temos que lembrar que estamos transformando a matriz na matriz identidade e a matriz identidade possui todos os elementos da diagonal principal iguais a .
Olhando a nossa matriz, vemos que na primeira linha temos aquele ali estragando tudo. Vamos transformá-lo em dividindo toda essa linha por 3:
Não esquece de fazer na matriz ao lado também, hein!!
Opa!!! Olha só quem apareceu na matriz da esquerda. Nossa matriz se transformou na matriz identidade . Então concluímos os dois passos do procedimento de inversão! Ebaaa!
Você ainda não percebeu, mas a gente já encontrou ca matriz inversa! Olha aquela matriz da direita:
Essa daqui é a matriz inversa da nossa matriz A! A gente viu lá em cima que o produto da matriz A por essa matriz que obtivemos agora resulta na matriz identidade!!
Vai ser sempre assim, galera. Calculamos a inversa de uma matriz quadrada escrevendo a matriz inversa correspondente ao lado da nossa matriz original. Realizamos os dois passos do procedimento de inversão e no final, a matriz identidade que a gente escreveu ao lado se torna a nossa matriz inversa!
Agora, para a gente ficar fera em inverter matrizes, precisamos praticar. Estarei lá nos exercícios te esperando 😊
Procedimento para inverter uma matriz
Exercícios Resolvidos
Exercício Resolvido #1
Apostila Álgebra Linear
Verifique se a matriz e a matriz são inversas entre si.
Passo 1
Faaaala galerinhaa !! Prontos para começar mais uma seção?!
Antes de começar precisamos nos perguntar, como sabemos se duas matrizes são inversas?
Quando a multiplicação entre elas origina uma matriz identidade. Isso quer dizer que se multiplicarmos as duas, vamos ter que ter essa resposta aqui
Essa matriz que só tem 1 na diagonal e 0 fora da diagonal é o que a gente chama de matriz identidade.
Então, vamos multiplica-las e ver no que dá, ok?
Quem aí sabe como multiplicar matrizes?
Parece difícil, mas não é ! Vamos multiplicar cada a linha por cada coluna, ok?
Melhor vermos na prática que vai ficar mais claro. Vamos começar com a primeira linha da matriz A e a primeira coluna da matrix B
Realizando as operações, a gente tem o primeiro elemento da primeira linha da nossa matriz resposta:
Agora a gente faz para as demais linhas e colunas para obter os outros elementos da matriz resposta:
Realizando as operações, temos
Isso aí não está com cara de identidade, não né ?!
Então, A e B não são inversas entre si !!
Resposta
Exercício Resolvido #2
Apostila Álgebra Linear
Verifique se a matriz e a matriz são inversas entre si.
Passo 1
Vamos começar mais uma?!
Já sabemos que para duas matrizes serem inversas uma da outra a multiplicação entre elas origina uma matriz identidade, ou seja, a gente tem que ter isso aqui como resposta:
Então, vamos multiplica-las e ver no que dá, ok?
Quem aí sabe como multiplicar matrizes?
Parece difícil, mas não é ! Vamos multiplicar cada a linha por cada coluna, ok?
Melhor vermos na prática que vai ficar mais claro:
Realizando as operações:
Isso sim é uma identidade !!
Então, A e B são inversas entre si !!
Resposta
Exercício Resolvido #3
Apostila Álgebra Linear
Seja . Determine a sua inversa.
Passo 1
Bora seguir ?!
Já sabemos que para duas matrizes serem inversas uma da outra a multiplicação entre elas origina uma matriz identidade, vamos ver?
E como faremos para achar ?
Bom galerinha, temos um procedimento bem simples para achar isso, não é? Basta colocarmos a matriz identidade ao lado da nossa matriz original:
E agora vamos escalonar esta matriz A até chegarmos na forma reduzida. Só não podemos esquecer que tudo que a gente fizer com a matriz A temos que fazer com a identidade, tudo bem?
Se lembram da forma reduzida?
Então vamos começar?
Passo 2
Na matriz A, o já está no lugar certo, então que tal zeramos este 3 logo abaixo fazendo a operação:
Então:
Para chegar na forma reduzida, este também precisa se transformar em :
Então:
Agora, este na primeira linha também precisa zerar:
Então:
Quando nós chegamos neste ponto o que obtemos é:
Sendo assim, a matriz inversa da matriz A é o que resultou no lado direito:
Shoow de bolinhas !!
Resposta
Exercício Resolvido #4
Exercícios – UFPEL
Seja . Determine a sua inversa.
Passo 1
Animados para continuar?!
Espero que sim ein !!
Já sabemos que para duas matrizes serem inversas uma da outra a multiplicação entre elas origina uma matriz identidade, vamos ver?
E como faremos para achar ?
Bom galerinha, temos um procedimento bem simples para achar isso, não é? Basta colocarmos:
Agora vamos escalonar esta matriz A, e consequentemente a identidade, até chegarmos na forma reduzida !!
Então vamos começar?
Passo 2
Para começar podemos trocar as linhas e de lugar, para aparecer o pivô da primeira coluna, ok?
Então:
O já está no lugar certo, então que tal zeramos este logo abaixo fazendo a operação:
Então:
Para chegar na forma reduzida, este também precisa se transformar em :
Então:
Agora, este também precisa zerar:
Então:
Quando nós chegamos neste ponto o que obtemos é:
Sendo assim, a matriz esquisita que fica no lado direito das nossas operações é a inversa que queríamos
Shoow de bolinhas !!
Resposta
Exercício Resolvido #5
Exercícios – UFPEL
Seja . Determine a sua inversa.
Passo 1
Mais uma bem parecida com a anterior, não é?
Vamos ver se vocês já estão feras !!
Já sabemos que existe um procedimento bem simples para achar a inversa, não é? Basta colocarmos:
E escalonar a matriz A até a forma reduzida sem esquecer de fazer as mesmas operações com a matriz identidade que está na direita!!
Então vamos começar?
Passo 2
Para começar vamos transformar o em pivô da linha , ok?
Então:
O já está no lugar certo, então que tal zeramos este 11 logo abaixo fazendo a operação:
Então:
Para resolver este termo , vamos passar o multiplicando pelo e depois realizar a operação:
Então:
Para chegar na forma reduzida, este também precisa se transformar em :
Então:
Agora, este também precisa zerar:
Então:
No termo , como o denominador é igual podemos simplesmente somar os numeradores:
Quando nós chegamos neste ponto o que obtemos é:
Sendo assim, a matriz resultante ali do lado direito é a nossa matriz inversa
Shoow de bolinhas !!
Resposta
Exercício Resolvido #6
Exercícios – UFPEL
Seja . Determine a sua inversa, se existir.
Passo 1
Bora continuar ?
Bom galerinha, esse se existir é importante, porque uma matriz só tem inversa quando seu determinante é diferente de zero !! Ou seja:
Para calcular o determinante em uma matriz do tipo:
Basta fazermos a operação:
Então:
Então, não existe uma matriz inversa !! Quando isso acontece, dizemos A é uma matriz singular !
E o nosso problema acabou assim !!
Resposta
Exercício Resolvido #7
Exercícios - UNESP
Encontre a inversa da matriz abaixo, se existir:
Passo 1
Mais uma bem legalzona pra gente se divertir !!
Bom galerinha, esse se existir é importante, porque uma matriz só tem inversa quando seu determinante é diferente de zero !! Ou seja:
Para calcular o determinante nós vamos colocar as colunas e ao lado da matriz, desse jeito:
Depois nós vamos traçar linhas, da seguinte forma:
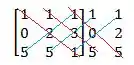
A multiplicação dos números ao longo das linhas vermelhas será positiva, enquanto as azuis negativas ! E para achar o determinante é só somar tudo:
Então, existe uma matriz inversa !!
Passo 2
Já vimos que a matriz inversa pode ser calculada colcando e quando transformamos A em identidade acharemos certo?
Então:
Para transformar A em sua forma reduzida, vamos começar zerando esse que está ali na primeira coluna:
Então:
Agora, precisamos transformar este em pivô, ou seja, em
Então:
Na coluna ainda temos que transformar o em zero:
Então:
Agora, precisamos fazer aparecer o pivô da terceira coluna:
Então:
E para finalizar daremos um jeitinho de zerar e
Então:
Quando nós chegamos neste ponto o que obtemos é:
Sendo assim,
Shoow de bolinhas !!
Resposta
Exercício Resolvido #8
Exercícios - UNESP
Encontre a inversa da matriz abaixo, se existir:
Passo 1
Vamos que vamos ?!
Bom galerinha, esse se existir é importante, porque uma matriz só tem inversa quando seu determinante é diferente de zero !! Ou seja:
Para calcular o determinante nós vamos colocar as colunas e ao lado da matriz, desse jeito:
Depois nós vamos traçar linhas, da seguinte forma:

A multiplicação dos números ao longo das linhas vermelhas será positiva, enquanto as azuis negativas ! E para achar o determinante é só somar tudo:
Então, existe uma matriz inversa !!
Passo 2
Já vimos que a matriz inversa pode ser calculada colcando e quando transformamos A em identidade acharemos certo?
Então:
Para transformar A em sua forma reduzida, vamos começar zerando esse e que estão ali na primeira coluna:
Então:
Agora, precisamos achar o pivô da segunda coluna e para isso vamos transformar este em pivô, ou seja, em
Então:
Na coluna ainda temos que transformar o e em zero:
Então:
Agora, precisamos fazer aparecer o pivô da terceira coluna:
Então:
E para finalizar daremos um jeitinho de zerar os
Então:
Quando nós chegamos neste ponto o que obtemos é:
Sendo assim,
Shoow de bolinhas !!
Resposta
Exercício Resolvido #9
Apostila Álgebra Linear - UFRGS
Encontre a inversa da matriz abaixo:
Passo 1
Bora seguir ?!
Como faremos para achar ?
Bom galerinha, temos um procedimento bem simples para achar isso, não é? Basta colocarmos a matriz identidade ao lado da nossa matriz original:
E agora vamos escalonar esta matriz A até chegarmos na forma reduzida. Só não podemos esquecer que tudo que a gente fizer com a matriz A temos que fazer com a identidade, tudo bem?
Se lembram da forma reduzida?
Então vamos começar?
Passo 2
Na matriz A, o já está no lugar certo, então que tal zeramos este logo abaixo fazendo a operação:
Então:
Para chegar na forma reduzida, este também precisa se transformar em :
Então:
Agora, este na primeira linha também precisa zerar:
Então:
Para realizar aquela subtração ali, temos que fazer o seguinte:
Quando nós chegamos neste ponto o que obtemos é:
Sendo assim, a matriz inversa da matriz A é o que resultou no lado direito:
Shoow de bolinhas !!
Resposta
Exercício Resolvido #10
Apostila Álgebra Linear - UFRGS
Encontre a inversa da matriz abaixo:
Passo 1
Bora seguir ?!
Como faremos para achar ?
Bom galerinha, temos um procedimento bem simples para achar isso, não é? Basta colocarmos a matriz identidade ao lado da nossa matriz original:
E agora vamos escalonar esta matriz A até chegarmos na forma reduzida. Só não podemos esquecer que tudo que a gente fizer com a matriz A temos que fazer com a identidade, tudo bem?
Se lembram da forma reduzida?
Então vamos começar?
Passo 2
Na matriz A, o já está no lugar certo, então que tal zeramos este logo abaixo fazendo a operação:
Então:
Quando nós chegamos neste ponto o que obtemos é:
Sendo assim, a matriz inversa da matriz A é o que resultou no lado direito:
Shoow de bolinhas !!