Transformações Lineares
Teoria
Faaala, Aí! Vamos aprender aqui sobre uma operação que podemos fazer nos espaços vetoriais, as chamadas transformações lineares. A ideia é bem simples de se ver. Essas transformações são funções (com algumas regras) que vão pegar um vetor do nosso espaço e transformá-lo em algum vetor diferente.
Vamos refinar esse conceito para conseguirmos trabalhar melhor isso!!
Introdução
Para entendermos as transformações lineares, vamos precisar de dois espaços vetoriais que eu vou chamar de e . Esses espaços podem ou não serem o mesmo espaço vetorial, mas aqui eu quis chamar de nomes diferentes só para a gente não se confundir, beleza. A ideia está representada nessa imagem aqui:

A transformação linear vai ser uma aplicação de uma operação (a gente usa letras maiúsculas para nomear as transformações também) em algum vetor do meu espaço vetorial , por exemplo, no vetor , que vai me fornecer um outro vetor, , no outro espaço vetorial . Podemos ver esse funcionamento na imagem a seguir:
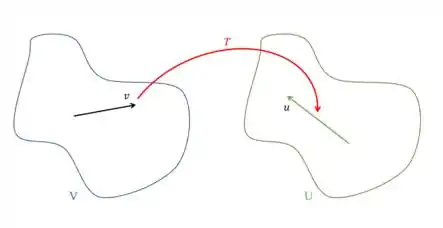
Na prática, a gente fala que é uma transformação linear que pega um vetor no espaço e leva para um outro vetor no espaço através desse código aqui:
A gente vai se deparar muito com isso, então é bom já termos em mente.
Transformações de para
Vamos ver alguns exemplos de transformações aqui para a gente já ficar acostumado.
Considere a seguinte transformação linear :
Epa! Que assustador!!
Calma, vamos traduzir isso tudo aí juntos.
Essa transformação pega um vetor do (um vetor que tem duas componentes) e nos dá como resposta um vetor do (um vetor com três componentes). Vamos ver como que ela atua, por exemplo, no vetor
Para fazermos isso, temos que substituir (x sempre vai ser o primeiro número do parêntesis) e ( vai ser sempre o segundo número do parêntesis) naquela fórmula que o problema nos passou:
Calculando o produto que apareceu ali e a soma, ficamos com
Olha lá! Saímos do vetor , que possui duas componentes, para o vetor que possui três componentes. É assim que funciona!
Outra transformação aí para a gente ver: dado por
Aqui temos uma transformação que pega um vetor de um espaço e nos dá um vetor do mesmo espaço. Bem parecido com aquelas funções do segundo grau, né? A ideia é a mesma, pegamos um valor de e a transformação vai nos fornecer o resultado de .
Olha, até agora eu só mostrei para vocês algumas transformações. Mas as que a gente está interessado são as transformações lineares. Essas transformações possuem algumas regras que elas devem seguir. Então, pode ser que nos exemplos que a gente viu, tenhamos ou não transformações lineares. Vamos ver essas regras agora!!
Propriedades das Transformações Lineares
Para que uma transformação seja uma transformação linear, ela deve satisfazer:
- Para quaisquer e do espaço vetorial , a transformação da soma desses vetores deve ser igual a soma das transformações de cada vetor separadamente:
- Para qualquer no espaço e qualquer número real , a transformação do produto tem que ser igual a vezes a transformação de :
Com isso tudo em mente, vamos ver se aquelas transformações que a gente viu aqui são lineares ou não.
Testando se uma transformação é ou não linear
Vamos começar com a transformação :
Para verificarmos se ela respeita as duas propriedades das transformações lineares, vamos precisar supor dois vetores de quaisquer:
E um número real também qualquer.
Vamos começar pela primeira propriedade. Calculamos primeiro e depois calculamos e vemos se os resultados batem. Para calcularmos ajuda calcularmos primeiro o resultado da soma :
Somando cada componente, temos:
Boa!
Agora, podemos calcular:
Usando a fórmula de que o problema nos deu substituindo por e por . Dessa forma, ficamos com:
Realizando aquele produto de ali em ambos os termos do parêntesis, temos
Essa é a forma final de .
Agora, vamos usar as transformações de cada vetor isoladamente:
Temos que somar esses dois resultados:
Somando cada componente isoladamente, temos:
Arrumando os termos, já que a ordem dos fatores não altera a soma:
E essa é a forma final de . E aí a gente vê que
Primeira propriedade tá valendo 😊
Vamos para a segunda propriedade!
Agora, temos que calcular . Primeiro vamos ver como que fica :
Multiplicando em cada uma das componentes, ficamos com
Usando a fórmula de que o problema nos deu substituindo por e por , ficamos com:
Podemos por em evidência:
Como em todas as componentes eu tenho um multiplicando (a gente pode pensar que ), podemos por o em evidência de tudo:
Opaaa! Olha aquele vetor que apareceu ali no lado direito desta igualdade! Vê se não é exatamente o valor de que já calculamos acima. Então, podemos escrever
E vemos que a segunda propriedade também bate. Então, esse que o problema nos deu é sim uma transformação linear!
Vamos ver se dado por
é uma transformação linear.
Bom, a gente pode começar testando qualquer uma das propriedades. Vamos começar pela segunda? Vamos lá!
Antes, deixa só eu te dar uma dica. O nome linear que aparece aqui direto tem a ver com o fato da transformação só carregar termos de (ou mais) elevados à 1. Então, quando se deparar com alguma transformação que envolva ou , já suspeita que não vai ser uma transformação linear, ok?
Vamos lá testar essa segunda propriedade. Primeiro, vamos supor um vetor qualquer:
Com isso, usando a fórmula de que o problema nos deu podemos escrever:
Agora, precisamos calcular , primeiro vemos que
Vamos calcular a transformação disso aí usando a fórmula que o problema nos deu substituindo por :
Quando temos um produto elevado ao quadrado, podemos elevar ambos os termos do produto ao quadrado e tirar aqueles parêntesis:
Beleza! Agora vamos ver se isso é igual a . Usando o valor de que já calculamos agora há pouco, temos
Como a ordem dos fatores não altera o produto, podemos trocar o e o de lugar:
Se compararmos os valores de com o de vemos que eles são diferentes, então, nesse caso temos:
Isso viola a nossa segunda propriedade, então essa transformação não pode ser linear. #quepena
É isso, galera. Chegamos ao fim desse tópico. Mas não tem jeito, temos que dar uma treinada para ficarmos bem safos nessas transformações lineares!!
Vem comigo para resolvermos uns exercícios? Te espero lá 😊
Propriedades das Transformações Lineares
Testando se uma transformação é ou não linear
Exercícios Resolvidos
Exercício Resolvido #1
Teste de conhecimento Transformação Linear 5 – Estácio
Determine a imagem do vetor pela Transformação Linear
Passo 1
Faaaaala aí! Tudo certinho? Vamos para cima dessa questão sobre Transformação Linear!
Bom, a Transformação Linear tem essa carinha aqui:
É uma transformação
A gente tem que nosso domínio é
E queremos saber a imagem, ou seja, o resultado transformação:
A gente já pode ver, pelo jeitinho da transformação, que a segunda coordenada vai ser zero, independentemente do valor de e . Isso já elimina algumas opções da questão 😊
Passo 2
Show de bola, vamos então resolver isso daí!
Temos que
E queremos
Então o que vamos fazer é substituir onde tem por e onde tem por
Vamos lá então:
Vamos fazer a multiplicação!
Então nossa transformação fica:
Que é a letra e!
Resposta
e)
Exercício Resolvido #2
Álgebra Linear – 3 teste de conhecimento – Estácio
Determine a imagem do vetor pela transformação linear
Passo 1
Opa, e aí! Vamos pra cima dessa questão sobre Transformação Linear!
Bom, a Transformação Linear tem essa carinha aqui:
É uma transformação
A gente tem que nosso domínio é
E queremos saber a imagem, ou seja, o resultado da transformação
Passo 2
Show de bola, vamos então resolver isso daí!
Temos que
E queremos
Então o que vamos fazer é substituir onde tem por e onde tem por
Vamos lá então:
Fazendo as multiplicações, temos:
Somando, ficamos com:
Show, achamos bonitinho a resposta, só precisávamos substituir! Vamos continuar exercitando para ficar fera nessas transformações
Resposta
d)
Exercício Resolvido #3
Álgebra linear – teste de conhecimento 6 – Estácio
Determine a imagem do vetor pela Transformação Linear
Passo 1
Faaaaala aí! Vamos pra cima dessa questão sobre Transformação Linear? Vamo que vamo!
Bom, a Transformação Linear tem essa carinha aqui:
É uma transformação
A gente tem que nosso domínio é
E queremos saber a imagem, ou seja, a transformação
Passo 2
Show de bola, vamos então resolver isso daí!
Temos que
E queremos
Então o que vamos fazer é substituir onde tem por e onde tem por
Vamos lá então:
Vamos começar fazendo as multiplicações!
Agora, como com dá , ficamos com:
Isso dá pra gente:
Que é a letra c
Resposta
c)
Exercício Resolvido #4
Álgebra linear – teste de conhecimento 5 – Estácio
Determine a imagem do vetor pela Transformação Linear
Passo 1
Faaaaala aí! Tudo certinho? Vamos pra cima dessa questão sobre Transformação Linear!
Bom, a Transformação Linear tem essa carinha aqui:
A gente já pode ver, pelo jeitinho da transformação, que a segunda coordenada vai ser zero, independentemente do valor de , e . Isso já elimina uma opçãozinha da questão 😊
É uma transformação
A gente tem que nosso domínio é
E queremos saber a imagem, ou seja, a transformação
Passo 2
Show de bola, vamos então resolver isso daí!
Temos que
E queremos
Então o que vamos fazer é substituir onde tem por , onde tem por e onde tem por
Vamos lá então:
Show, achamos bonitinho a resposta, só precisávamos substituir! Vamos continuar exercitando para ficar fera nessas transformações
Resposta
Exercício Resolvido #5
Teste 5 de conhecimento Transformação Linear – Estácio
Determine a imagem do vetor pela Transformação Linear
Passo 1
Opa, tudo certinho? Vamos pra cima dessa questão sobre Transformação Linear!
Bom, a Transformação Linear tem essa carinha aqui:
É uma transformação
A gente tem que nosso domínio é
E queremos saber a imagem, ou seja, a transformação
Passo 2
Show de bola, vamos então resolver isso daí!
Temos que
E queremos
Então o que vamos fazer é substituir onde tem por , onde tem por e onde tem por
Vamos lá então:
Beleza, somando isso vamos ficar com:
Que é a letra
Resposta
d)
Exercício Resolvido #6
Complementos de Álgebra Linear – UNIP
Seja , linear dada por determinar a imagem dos vetores pela transformação
Passo 1
Opa, e aí! Vamo que vamo para mais uma questão de transformação linear!
Querides, a primeira Transformação Linear tem essa carinha aqui:
É uma transformação
Passo 2
Show, já vimos a transformação linear, agora vamos começar com a opção i), a gente tem que nosso domínio é
E queremos saber a imagem, ou seja, a transformação
Show de bola, vamos então resolver isso daí!
Temos que
E queremos
Então o que vamos fazer é substituir onde tem por , onde tem por e onde tem por
Vamos lá então:
Vamos começar fazendo a multiplicação
Beleza, somando isso vamos ficar com:
Passo 3
Agora vamos para a ii) aqui temos que o domínio é
E queremos saber a imagem, ou seja, a transformação
Vamos fazer de forma análoga ao passo anterior!
Temos que
E queremos
Então o que vamos fazer é substituir onde tem por , onde tem por e onde tem por
Vamos lá então:
Vamos começar fazendo a multiplicação
Beleza, somando isso vamos ficar com:
Então a gente consegue ver que uma transformação pode ter infinitas imagens, depende do vetor que queremos analisar!
Resposta
Exercício Resolvido #7
Teste de conhecimento 6 Transformação Linear – Estácio
Seja e uma transformação linear associa vetores pertencente a com pertencente a . Seja a lei que define a transformação dada por , o valor de é:
- Nenhuma das respostas acima
Passo 1
Opa, fala aí galerinha! Vamos seguir com nossos estudos sobre Transformação Linear.
Bom o enunciado dá várias informações pra gente, vamos analisá-las a seguir:
Temos uma transformação de um vetor com duas coordenadas para um vetor com três coordenadas .

Pode sim Galvão, podemos encontrar transformações de coordenadas diferentes!
Além disso, temos que a transformação tem essa carinha aqui:
E o domínio que ele dá pra gente é o vetor do
E ele vai retornar pra gente o vetor que queremos descobrir que vai ser da forma
Porque depois de passar pela transformação, ele vai estar no
Passo 2
Show de bola, agora que a gente já entendeu o que está acontecendo vamos partir pra cima da nossa questão. Lembrando que a transformação é:
E queremos
Então o que vamos fazer é substituir onde tem por e onde tem por
Vamos lá então:
Fazendo essas continhas, temos que
Que é a letra
Resposta
b)
Exercício Resolvido #8
Questões Álgebra Linear – UNIP
Dentre as transformações definidas pelas seguintes leis, verificar quais são lineares:
c)
Passo 1
Faaaaaaaala aí! Vamo que vamo para mais uma questão sobre Transformação Linear
Nesse exercício precisamos verificar se a transformação respeita as condições para serem uma . Vamos lembrar aqui quem são essas condições:
Vamos começar então ;)
Passo 2
Para verificar se uma transformação é linear ou não, a gente sempre começa supondo dois vetores quaisquer:
Outra coisa importante de relembrar é que na soma de dois vetores a gente soma as componentes assim:
Agora a gente já pode partir para a transformação do problema. Pela primeira condição, precisamos que:
Vamos começar desenvolvendo o lado da direita da equação, lembrando que
Então
A gente precisa somar essas duas transformações:
Somando cada componente, ficamos com
Beleza!! Agora a gente desenvolve o lado esquerdo da nossa equação. Lembrando de novo que
Então, substituindo por e por
Fazendo a o produto notável, temos que:
Passo 3
Agora a gente tem que comparar os dois resultados e ver se são iguais:
Opa, deu diferente! A gente consegue ver que:
Como não atende a primeira condição, podemos afirmar que a transformação não é linear
Vamos continuar treinando para ficar fera!
Resposta
não é linear
Exercício Resolvido #9
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 126 – Fix 4.1.
Determine se é uma transformação linear :
Passo 1
Opa, tudo bem? Vamo que vamo para mais uma questão sobre Transformação Linear
Nesse exercício precisamos verificar se a transformação respeita as condições para ser uma . Vamos lembrar aqui quem são essas condições:
Vamos começar então ;)
Passo 2
Para verificar se uma transformação é linear ou não, a gente sempre começa supondo dois vetores quaisquer:
Outra coisa importante de relembrar é que na soma de dois vetores a gente soma as componentes assim:
Agora a gente já pode partir para a transformação do problema. Pela primeira condição, precisamos que:
Vamos começar desenvolvendo o lado , lembrando que
Então
Precisamos calcular a soma dessas duas transformações:
Somando os vetores, ficamos com
Beleza, já temos um lado da primeira condição que devemos testar!
Desenvolvendo o lado , lembrando de novo que
Então, substituindo por e por
Fazendo a distributiva, temos que:
Passo 3
Agora a gente precisa ver se os dois lados que calculamos são iguais:
Opa!! Tanto a igualdade de cima quanto a de baixo conferem! Então ela é linear? Não!!
Temos que verificar a segunda condição antes de podermos afirmar algo.
Passo 4
Desenvolvendo o lado lembrando que
Então, substituindo por e por temos:
Desenvolvendo o lado lembrando de novo que
Temos então:
Colocando o vetor da nossa transformação, temos:
Fazendo a distributiva ficamos com:
Passo 5
Comparando e , temos que
Opa, igualzinho! Assim, podemos ver que .
Portanto, provamos que as duas condições da linearidade satisfazem a nossa transformação! Logo, podemos dizer que ela é uma transformação linear.
Resposta
é linear.
Exercício Resolvido #10
Lista de exercícios Transformação Linear – Álgebra – UNIP (adaptada)
A transformação é linear. Sabendo que e , determine
Passo 1
Faaaala aí, tudo certinho? Vamos pra cima de mais uma questão sobre Transformação Linear!
O enunciado dá pra gente a transformação de dois vetores
E
E pede pra gente a transformação de outro vetor
Show, como a transformação é linear (não precisamos provar porque o enunciado diz pra gente) vamos usar alguma propriedade das transformações lineares para conseguirmos usar esses resultados que o exercício nos deu em nosso favor!
Vamos fazer operações com os vetores que temos para achar o vetor que não conhecemos a transformação. Desse jeitinho aqui:
Fazendo a distributiva no lado esquerdo:
Mas pra que isso? Bom, como a transformação é linear vamos usar suas propriedades a nosso favor!! Olha só, a gente quer calcular certo? Se a gente usar essa combinação aqui de cima, olha só como isso vai ficar:
Beleza, não ajudou muito ainda né? Mas olha só, como é uma T.L. a gente tem essas propriedades aqui:
Se a gente aplicar a primeira propriedade em que a gente obteve ali, a gente fica com:
Se botarmos tanto o quanto o em evidência, temos
E usando a segunda propriedade de
Opa!!!!
A gente sabe que e então a nossa transformação fica com essa carinha aqui
Beleza!! Só precisamos achar quem é o e quem é o !
Passo 2
Show, voltando um pouco, nós conseguimos escrever que
Somando os vetores, temos que:
Isso dá um sisteminha pra gente, desse jeito aqui:
Opa, a primeira linha já entrega pra gente o valor de , entao temos que
Agora para achar só precisamos colocar o valor de na linha de baixo!
Passando pro outro lado, temos:
Show, achamos os valores de e !
Passo 3
Beleza agora vamos pegar esses coeficientes e substituir na expressão que a gente obteve para .
Substituindo os valores dos coeficientes, temos:
Fazendo as multiplicações, temos:
Belezinha??