Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 7.2 - Ex. 4

Nos Exercícios 2–9, encontre uma matriz P que diagonaliza A ortogonalmente e determine P - 1 A P .

A = 6 - 2 - 2 3

Passo 1

Para achar a matriz P vamos calcular os autovalores e autovetores. Relembrando

A u t o v a l o r e s   ( λ ) :   A - λ I = 0

A u t o v e t o r e s   ( v ) :   A - λ I v = 0

Passo 2

Primeiro vamos fazer o autovalor

  A - λ I = 0

λ I = 1 0 0 1 ∙ λ

λ I = 1 ∙ λ 0 ∙ λ 0 ∙ λ 1 ∙ λ

λ I = λ 0 0 λ

Passo 3

Retornando para

λ I - A = 0

Substituindo os valores

λ I - A = λ 0 0 λ - 6 - 2 - 2 3

Reescrevendo

λ I - A = λ - 6 2 2 λ - 3

Então, temos

λ - 6 2 2 λ - 3 = 0

Calculando o determinante, lembrando que para uma matriz 2 × 2 , multiplicamos os elementos da diagonal principal e subtraímos do resultado da multiplicação dos elementos da diagonal secundária

λ - 6 ∙ λ - 3 - 4 = 0

λ 2 - 3 λ - 6 λ + 18 - 4 = 0

λ 2 - 9 λ + 14 = 0

Passo 4

Determinando os autoespaços

λ 2 - 9 λ + 14 = 0

λ = - b ± Δ 2 a

Onde

Δ = b 2 - 4 a c

Passo 5

Calculando

Δ = b 2 - 4 a c

Δ = ( - 9 ) 2 - 4 ∙ 1 ∙ 14

Δ = 25

Retornando em

λ = - - 9 ± 25 2 ∙ 1

λ = 9 ± 5 2

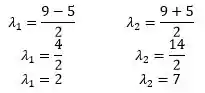
Passo 6

Determinando os autovetores

A - λ I v = 0

Onde

v = x y

Logo

A - λ I ∙ x y = 0

Como já temos A - λ I

λ - 6 2 2 λ - 3 ∙ x y = 0

Vamos substituir os valores encontrados dos autovalores para determinar v .

Passo 7

Para λ 1 = 2

2 - 6 2 2 2 - 3 ∙ x y = 0

- 4 2 2 - 1 ∙ x y = 0

Montando em forma de sistema, temos

- 4 x + 2 y = 0 2 x - y = 0

Temos que

4 x = 2 y

x = 2 y 4

x = y 2

Escrevendo

v = x y

v 1 = y 2 y

Colocando y em evidência, temos

v 1 = y ∙ 1 2 1

Temos que o valor de autovetor é

v 1 = 1 2 1

Passo 8

Para λ 2 = 7

7 - 6 2 2 7 - 3 ∙ x y = 0

1 2 2 4 ∙ x y = 0

Montando em forma de sistema, temos

x + 2 y = 0 2 x + 4 y = 0

Temos que

x 2 y = 0

x = - 2 y

Escrevendo

v = x y

v 2 = - 2 y y

Colocando y em evidência, temos

v 2 = y ∙ - 2 1

Temos que o valor de autovetor é

v 2 = - 2 1

Passo 9

Agora vamos normalizar os autovetores

u 1 = v 1 v 1

u 1 = 1 1 2 2 + 1 2 ∙ 1 2 1

u 1 = 1 1 4 + 1 ∙ 1 2 1

u 1 = 1 1 4 + 4 4 ∙ 1 2 1

u 1 = 1 5 4 ∙ 1 2 1

u 1 = 1 5 2 ∙ 1 2 1

Podemos reorganizar a fração 1 5 2

u 1 = 2 5 ∙ 1 2 1

u 1 = 2 2 5 2 5

u 1 = 1 5 2 5

u 2 = v 2 v 2

u 2 = 1 - 2 2 + 1 2 ∙ - 2 1

u 2 = 1 4 + 1 ∙ - 2 1

u 2 = 1 5 ∙ - 2 1

u 2 = - 2 5 1 5

Passo 10

Para escrever P , colocamos os autovetores normalizados que diagonaliza A ortogonalmente em colunas

P = 1 5 - 2 5 2 5 1 5

Passo 11

Determinando P - 1 A P

Primeiro vamos determinar P - 1 , considerando ser uma matriz ortogonal

P - 1 = P T

P T = 1 5 2 5 - 2 5 1 5

Passo 12

Retornando para

P - 1 A P

E como P é ortogonal, então

P T A P

P T A P = 1 5 2 5 - 2 5 1 5 ∙ 6 - 2 - 2 3 ∙ 1 5 - 2 5 2 5 1 5

Passo 13

Relembrando como realizar a multiplicação entre matrizes: multiplica a linha da primeira matriz pela linha da segunda matriz e soma-os

G = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 e H = b 11 b 12 b 13 b 21 b 22 b 23 b 31 b 32 b 33

G ∙ H = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∙ b 11 b 12 b 13 b 21 b 22 b 23 b 31 b 32 b 33

= a 11 b 11 + a 12 b 21 + a 13 b 31 a 11 b 12 + a 12 b 22 + a 13 b 32 a 31 b 11 + a 32 b 21 + a 33 b 31 a 21 b 11 + a 22 b 21 + a 23 b 31 a 21 b 12 + a 22 b 22 + a 23 b 32 a 31 b 12 + a 32 b 22 + a 33 b 32 a 31 b 11 + a 32 b 21 + a 33 b 31 a 31 b 12 + a 32 b 22 + a 33 b 32 a 31 b 13 + a 33 b 23 + a 33 b 33

Passo 14

Calculando

P T A P = 1 5 2 5 - 2 5 1 5 ∙ 6 - 2 - 2 3 ∙ 1 5 - 2 5 2 5 1 5

P T A P = 1 5 ∙ 6 + 2 5 ∙ - 2 1 5 ∙ - 2 + 2 5 ∙ 3 - 2 5 ∙ 6 + 1 5 ∙ - 2 - 2 5 ∙ - 2 + 1 5 ∙ 3 ∙ 1 5 - 2 5 2 5 1 5

P T A P = 6 5 - 4 5 - 2 5 + 6 5 - 1 2 5 - 2 5 4 5 + 3 5 ∙ 1 5 - 2 5 2 5 1 5

P T A P = 2 5 4 5 - 1 4 5 7 5 ∙ 1 5 - 2 5 2 5 1 5

P T A P = 2 5 ∙ 1 5 + 4 5 ∙ 2 5 2 5 ∙ - 2 5 + 4 5 ∙ 1 5 - 14 5 ∙ 1 5 + 7 5 ∙ 2 5 - 14 5 ∙ - 2 5 + 7 5 ∙ 1 5

P T A P = 2 5 + 8 5 - 4 5 + 4 5 - 14 5 + 14 5 28 5 + 7 5

P T A P = 10 5 0 0 35 5

P T A P = 2 0 0 7

Resposta

P = 1 5 - 2 5 2 5 1 5

P T A P = 2 0 0 7

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para cada uma das seguintes matrizes simétricas A , encontrar uma matriz ortogonal P , para a qual P t A P seja diagonal. A = 2 2 2 5
Determinar uma matriz P que diagonaliza A ortogonalmente e calcular P - 1 A P . A = 0 0 2 0 - 1 0 2 0 0
Determinar uma matriz P que diagonaliza A ortogonalmente e calcular P - 1 A P . A = 3 - 1 1 - 1 5 - 1 1 - 1 3
Seja T :R 2 → R 2 o operador linear definido por T x , y = ( 7 x - 4 y ,- 4 x + y ) a) Determinar uma base do R 2 em relação à qual a matriz do operador é diagonal.b) Dar a matriz de T nessa base.
Para cada uma das seguintes matrizes simétricas A , encontrar uma matriz ortogonal P , para a qual P t A P seja diagonal. A = 2 2 2 2