É muito comum em problemas de engenharia terminar em sistemas de equações lineares do tipo:
Onde X é a variável a se descobrir, A os coeficientes que multiplicam variáveis e B algum vetor composto de valores constantes.
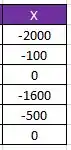
Um certo aluno resolvendo um problema de engenharia chegou nas determinadas matrizes:

Utilize as informações dadas em conjunto com a função linsolver que foi vista no curso para resolver o problema.
Passo 1
Se a gente analisar essa questão de forma genérica, esse é um problema bastante visto dentro da engenharia em diversas áreas.
A questão em si é um problema que se for analisado de forma genérica é um problema bastante visto dentro da engenharia em diversas áreas.
Equações lineares e suas resoluções são tão típicas dentro da engenharia quanto o estudante de engenharia e aquele famoso salgado do quiosque.
No matlab, o comando linsolver resolve equações lineares bem facinho, a gente só precisa informar pra ele quem é a Matriz dos Coeficientes (A) e quem é o vetor independente (b). Então o nosso primeiro passo vai ser inserir essa matriz e esse vetor.
A ideia aqui é inserir a Matriz dos coeficientes no Matlab em conjunto com a matriz b.
Após isso utilizar a função linsolver para resolver o sistema de equações lineares.
Passo 2
Passo 3
Se você analisar bem os coeficientes na tabela do enunciadoas matrizes, pode perceber que essas matrizeselas são matrizes repletas de zero (esparsas).
Então torna-se mais simples criar uma matriz e um vetor de zero e após isso substituir os elementos diferentes de zero.
Então:
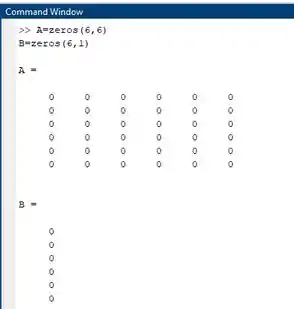
Se você digitou tudo certinho deve aparecer algo mais ou menos assim:
Analisando as matrizes novamente vemos quais que os elementos são diferentes de zero. Daí pra trocar o valor desses elementos, escrevemos o nome da matriz (no caso, é A) e à direita, entre parênteses, a linha e a coluna desse elemento. Pro elemento que fica na primeira linha e segunda coluna por exemplo, escrevemos A(1,2). E então igualamos cada um deles ao valor correto: são:
Analisando a matriz B temos que os elementos diferentes de zero são:
Implementando tudo no Matlab, deve aparecer algo assim:


Passo 4
Agora que as matrizes foram implementadas corretamente, apenas precisamos utilizar a função linsolver utilizando a seguinte sintaxe:
Primeiro tem que vir a matriz de coeficientes e depois o vetor independente.
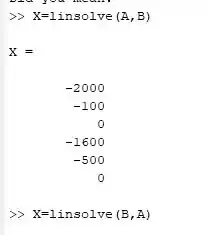
Onde nos dará o resultado igual a:
Passo 5
Resposta
E o resultado final é um vetor X cujo os elementos corresponde a: