Algumas funções úteis, vetores de células e estruturas.
Produzido por Gustavo BarbosaTeoria
Uma breve explicação...
Opaa, como você está? Espero que esteja tudo bem!
Vamos continuar nosso papo sobre vetores e matrizes no Matlab!
Imagine que você precisa criar um formulário cheio de informações de clientes como nome, CPF, RG, idade, estado civil e etc. Como você criaria isso no Matlab?
Ou até mesmo você está resolvendo um problema altamente complexo e precisa criar uma matriz de linhas por colunas (acredite, isso aparece com frequência em problemas de engenharia). Será que tem um jeito fácil de fazer isso?
São esses tipos de perguntas que iremos responder hoje, ok?
Criação de Matrizes.
Existe dentro do Matlab algumas funções destinadas a criação de matrizes de uma forma mais prática, essas funções se chamam função zero e função one.
A função zero cria uma matriz da ordem que você define, onde todos os elementos são preenchidos pelo número zero.
Já a função one é beeem parecida, ela cria uma matriz da ordem que você definir, mas aqui todos os elementos são o número 1.
A sintaxe de ambas é bastante similar, de forma geral fazemos:
Por exemplo, vamos criar uma matriz de zeros e outra de , ambas com linhas e colunas.
No Command Window do Matlab, escreva as seguintes informações:
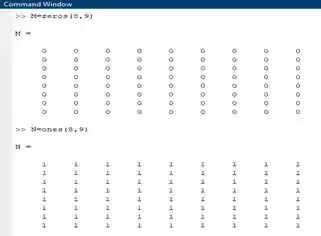
Tá, mas você deve estar se perguntando “para que serve esse tipo de matriz? ”
Em alguns problemas de engenharia, as resoluções de equações geram matrizes praticamente só de zeros, com apenas alguns elementos diferentes.
Logo é mais fácil criar a matriz de zeros e depois substituir os elementos dentro dela. Mas aí gera outra pergunta né? “Como faço para substituir elementos específicos assim? “
Então vamos para a próxima função matricial!
Substituição de elementos
Cada elemento de uma matriz que você cria no Matlab, a workspace armazena num lugar específico.
Por exemplo, imagina que você tem a seguinte matriz:
Analisando bem, podemos falar que os elementos da matriz correspondem a:
E se você escrever a matriz e colocar essas expressões no Matlab temos coisas do tipo:

Então, se o Matlab armazena cada elemento desse em uma posição específica, sabendo a posição podemos modificar aquele elemento específico, entende?
E é bem simples, voltando ao exemplo anterior quero trocar os zeros por , então é só fazer o seguinte:
E a nossa matriz vira:

De forma geral a sintaxe se torna:
E se você escrever , ele pega todos os elementos da linha e troca por , deixando nossa vida mais fácil na hora de modificar linhas ou colunas inteiras.
Matrizes e vetores de dados.
Matrizes ou vetores de dados, são aquelas que têm informações de mais de uma natureza, por exemplo uma matriz onde os elementos podem ser strings e variáveis inteiras.
E assim como o vetor ou matriz numérica podemos criar essa variável escrevendo elemento a elemento. Porém na matriz numérica os elementos eram escritos entre , e quando a matriz é de strings escreveremos entre .
Por exemplo, vamos supor que queremos armazenar algumas informações do Ganeff no banco de dados da empresa, então vamos escrever a parte string entre aspas simples como fazemos nas variáveis simples e os números, escrevemos normalmente. Lembrando que aqui, vamos usar :
E nos irá mostrar algo assim:
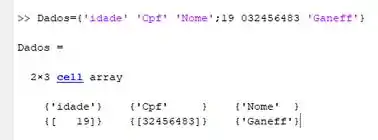
Porém mesmo entrando com alguns números, na saída do Matlab ele considera tudo como texto, e temos uma matriz de string, que recebe o nome de array.
Estruturas
A estrutura é um tipo de dado que permite o armazenamento de elementos de diferentes tipos. É como se criássemos uma workspace dentro da workspace.
Elas podem ser utilizadas com qualquer tipo de variável, porém em programações um pouco mais avançadas é comum a utilização para criar vetores de informação.
Mas como criamos essas coisas né?
Por exemplo, se queremos criar uma estrutura de informações para armazenar o nome do Ganeff e sua idade, então escrevemos assim:
Onde é o nome que demos a essa estrutura, é a função no matlab que cria a estrutura e dentro dos parênteses colocamos os dados que queremos guardar. Com isso, o Matlab irá fazer a seguinte coisa:

E se você for na workspace e dê dois cliques na variável , verá:

Nós criamos uma segunda Workspace dentro da própria Workspace.
De forma geral, a sintaxe dessa função é dada por:
Agora como operar essas informações né?
Uma vez que a estrutura está criada podemos inserir mais elementos dentro do vetor da seguinte forma:
Voltando ao exemplo anterior, queremos indicar também o de na forma de um string, então escrevemos o seguinte:
E o Matlab automaticamente faz:

Cada elemento da estrutura é identificado por um nome. Onde os arrays usam chave, aqui nas estruturas utilizamos a notação “.nome”
Logo precisamos apenas falar qual é a estrutura, colocar um ponto e o nome do dado que será inserido, após isso colocamos o igual e indicamos o dado normalmente. E assim vamos criando o vetor de informações dentro da estrutura!
Esse tipo de coisa é altamente utilizado em empresas, por exemplo, imagine que você está fazendo um cadastro numa loja e o atendente abre um portal e começa a te pedir informações.
Na realidade quando ele abre o portal, por trás daquela interface gráfica o código fonte cria uma estrutura dessa que vai ter o seu nome, após isso ele vai anexando informações dentro da estrutura com seu nome, criando assim um vetor ou uma matriz de informações.
Logo isso é bem útil para quem programa páginas, portais, planilhas de informação em sites e etc.
Bem, o assunto ficou extenso, mas espero que você tenha gostado. Ficaremos por aqui e até a próxima.
AAAAAAAH não se esqueça de dar uma olhadinha nos exercícios, é muito bom praticar essas coisas para gravar mais ainda na cabeça ok?
E ae esse texto te ajudou? Responde Aí.
Substituição de elementos
Matrizes e vetores de dados.
Estruturas
Exercícios Resolvidos
Exercício Resolvido #1
“Elaboração Própria”
Usando os comandos zeros e ones, crie uma matriz de três linhas e cinco colunas onde a primeira, segunda e quinta colunas sejam formadas de zeros e as demais colunas sejam formadas de um.
Passo 1
Iae ta tudo tranquilo?
Essa questão aqui é uma aplicação dos formulários que foram vistos na aula operações Matriciais.
O foco dela é simplesmente mostrar a você que com as funções zeros e ones podemos criar matrizes das mais variadas formas.
Então se analisarmos a questão a matriz que ela quer montar no Matlab é a seguinte:
Então vamos lá?
Passo 2
Antes de começar a brincar no Matlab precisamos saber como começar a fazer as coisas, para isso vamos olhar a matriz.
Ao analisá-la podemos observar que as colunas de número 1, 2 e 5 são nulas. E as demais são compostas por um.
E para criar essas matrizes só podemos usar as funções zeros e ones.
Ok. Agora que sabemos os ingredientes para montar o bolo, vamos começar a preparar.
Passo 3
Então para montar a matriz iremos precisar de uma matriz de 2 colunas e 3 linhas de zero, junto com uma matriz de 3 linhas e 1 coluna também nula.
Para isso escrevemos no command Window
A=zeros(3,2)
B=zeros(3,1)
Que deve resultar algo mais ou menos assim:

Após isso iremos precisar de uma matriz de 3 linhas e 2 colunas de 1.
Logo C=ones(3,2) resultando em:

Para completar o bolo só precisa juntar tudo em um recipiente só, para isso basta utilizar a forma comum que escrevemos as matrizes.
M=[A C B]
Onde nos revela a resposta final:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração Própria
Crie uma matriz A, onde todos os elementos sejam 1. Em seguida, adicione elementos à matriz A por anexação de elementos na matriz, tal que a matriz A transforme-se em:
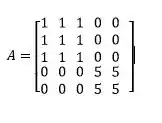
Obs: A anexação é trocar o elemento sob a forma A(1,2)=5, por exemplo.
Passo 1
Opa, está tudo tranquilo?
Bem, o enunciado em síntese pede para criar a matriz dada a partir de uma matriz base composta só de números 1.
Após criar a matriz 1, basta indexar os elementos que devem ser diferentes de 1 da seguinte forma:
Ou colocando um a um utilizando A(i,j)= algum valor
Ou podemos adiantar o Caminho lembrando que quando eu coloco : no lugar da linha ou coluna eu seleciono a linha ou a coluna toda da matriz.
Passo 2
Para a criação da matriz vamos utilizar a função ones, que cria uma matriz em que todos os elementos são iguais a 1. aAnalisando a matriz final como ela deve ser podemos notar que precisamos de uma matriz de 5 linhas e 5 colunas.
Então vamos criar uma matriz de 5 linhas e 5 colunas, porém uma é composta só de 1
B=ones(5,5)
Se escreveu tudo certinho deve mostrar algo assim:
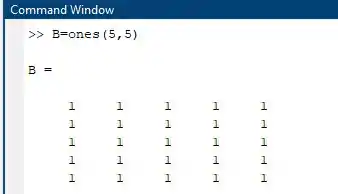
Passo 3
Uma vez que a matriz de 1 foi criada podemos modificar seus valores, se nósnos analisarmos vemos que tanto as linhas quanto as colunas 4 e 5 tem bastante zero. Então vamos zerar-las da seguinte forma:
B(4,:)=0
B(5,:)=0
Se você escreveu tudo certinho temos:

Agora vamos zerar as colunas:
B(:,4)=0
B(:,5)=0
Nos mostrando a seguinte Matriz:

Faltando trocar os valores do finalzinho para 5, para isso vamos escrever as seguintes expressões:
B(4,4)=5
B(4,5)=5
B(5,4)=5
B(5,5)=5
Com isso o Matlab monta a seguinte Matriz:

Que é a resposta da Questão.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração Própria
Ganeff um aluno de engenharia de Materiais realizou um experimento de uma análise termogravimétrica obtendo os seguintes dados experimentais:

Insira essa tabela no Matlab de forma organizada.
Passo 1
A ideia do exercício é começar a criar e brincar com os vetores e matrizes do tipo string.
A origem dos dados experimentais para esse exercício, porém, precisa inseri-los de forma organizada no Matlab.
Analisando a questão, precisamos criar dois vetores strings que é a primeira e a segunda linha da tabela, Após isso criar uma matriz numérica para no final unificar tudo.
Passo 2
Para criar os vetores strings basta lembrar que a variável é escrita como um string normal entre aspas simples.
Já na criação da matriz precisa se lembrar que uma matriz de strings os elementos ficam entre chaves em vez de colchetes.
Logo:
A={‘Time’ ‘Temp’ ‘DTA’ ‘TGA’ ‘DrTGA’}
B={‘sec’ ‘C’ ‘uV’ ‘mg’ ‘mg/sec’}
Após digitar tudo certinho deve aparecer algo do tipo:

Passo 3
Agora precisamos criar o Vetor Numérico, que podemos criar da mesma forma com que se criava antes:
M=[0 22.4313 0.0201 14.0091 7.10E-4; 1 22.4484 0.019 14.0102 0.0014; 2 22.4402 0.0206 14.0121 0.00174; 3 22.4784 0.022 14.0146 0.00145]
Porém para unificar precisamos transformar em strings, invés de utilizar as [] fica mais viável utilizar os {}
M={0 22.4313 0.0201 14.0091 7.10E-4; 1 22.4484 0.019 14.0102 0.0014; 2 22.4402 0.0206 14.0121 0.00174; 3 22.4784 0.022 14.0146 0.00145}
Uma vez que criamos os Vetores numéricos basta unificar tudo como um único Array, da seguinte forma:
ganeff={A;B;M}
Se digitou tudo certinho na sua janela deve mostrar algo assim:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração Própria
Devido a modernização com a chegada da internet e os microcomputadores as empresas foram obrigadas a se atualizar deixando de armazenar papéis e começar a criar cada vez mais bancos de dados para o armazenamento de informações.
Parabéns, você acabou de ser contratado como estagiário por uma empresa. E sua função é criar um banco de dados através da criação de uma estrutura para inserir os dados dos seguintes estagiários:
Nome: Julinha de Noronha
Cpf:545832181-10
Idade (anos): 25
Alguma reclamação: Nenhuma até o momento
Nome: Julio Alberto
Cpf:854798562-13
Idade (anos) : 19
Alguma reclamação: Chega sempre atrasado para o trabalho
Passo 1
A ideia aqui é que você acabou de ser contratado como estagiário e queremos implementar na Empresa um sistema de banco de dados através do Matlab.
O que você precisa fazer é criar uma estrutura de informações utilizando a função struct para cada um e inserir os dados principais que lhe foi informado pelos funcionários.
Logo, a ideia aqui é uma aplicação da função struct.
Passo 2
A criação dos bancos de dados é o mesmo para cada um o que muda são os dados pessoais dos funcionários, então o que explicamos aqui é válido igualmente para os demais passos:
Primeiramente vamos criar a estrutura da empresa com os dados de Julinha, para isso escrevemos:
Empresa_X=struct('Nome',{'Julinha de Noronha'},'Cpf',{'545832181-10'},'Idade',{'25 anos'},'Reclamacao',{'Nenhuma reclamação'})
Digitando tudo certinho deve aparecer algo assim:
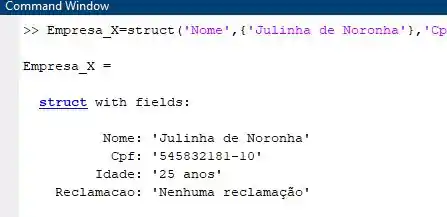
Passo 3
Utilizando a mesma função que utilizamos no de Julinha podemos criar também o banco de dados para Julio Alberto.
Empresa_X=struct('Nome',{' Julio Alberto’'},'Cpf',{'854798562-13'},'Idade',{'19 anos '},'Reclamacao',{' Chega sempre atrasado '})

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração Própria
É muito comum em problemas de engenharia terminar em sistemas de equações lineares do tipo:
Onde X é a variável a se descobrir, A os coeficientes que multiplicam variáveis e B algum vetor composto de valores constantes.
Um certo aluno resolvendo um problema de engenharia chegou nas determinadas matrizes:

Utilize as informações dadas em conjunto com a função linsolver que foi vista no curso para resolver o problema.
Passo 1
Se a gente analisar essa questão de forma genérica, esse é um problema bastante visto dentro da engenharia em diversas áreas.
A questão em si é um problema que se for analisado de forma genérica é um problema bastante visto dentro da engenharia em diversas áreas.
Equações lineares e suas resoluções são tão típicas dentro da engenharia quanto o estudante de engenharia e aquele famoso salgado do quiosque.
No matlab, o comando linsolver resolve equações lineares bem facinho, a gente só precisa informar pra ele quem é a Matriz dos Coeficientes (A) e quem é o vetor independente (b). Então o nosso primeiro passo vai ser inserir essa matriz e esse vetor.
A ideia aqui é inserir a Matriz dos coeficientes no Matlab em conjunto com a matriz b.
Após isso utilizar a função linsolver para resolver o sistema de equações lineares.
Passo 2
Se você analisar bem os coeficientes na tabela do enunciadoas matrizes, pode perceber que essas matrizeselas são matrizes repletas de zero (esparsas).
Então torna-se mais simples criar uma matriz e um vetor de zero e após isso substituir os elementos diferentes de zero.
Então:
Se você digitou tudo certinho deve aparecer algo mais ou menos assim:
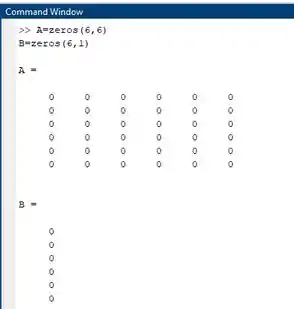
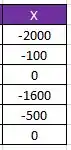
Analisando as matrizes novamente vemos quais que os elementos são diferentes de zero. Daí pra trocar o valor desses elementos, escrevemos o nome da matriz (no caso, é A) e à direita, entre parênteses, a linha e a coluna desse elemento. Pro elemento que fica na primeira linha e segunda coluna por exemplo, escrevemos A(1,2). E então igualamos cada um deles ao valor correto: são:
Analisando a matriz B temos que os elementos diferentes de zero são:
Implementando tudo no Matlab, deve aparecer algo assim:


Passo 3
Agora que as matrizes foram implementadas corretamente, apenas precisamos utilizar a função linsolver utilizando a seguinte sintaxe:
Primeiro tem que vir a matriz de coeficientes e depois o vetor independente.
Onde nos dará o resultado igual a:
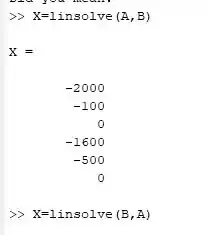
Resposta
E o resultado final é um vetor X cujo os elementos corresponde a: