A função abaixo serve para avaliar o polinômio quadrático :

Onde é um vetor com os coeficientes do polinômio e é o valor de para o qual queremos avaliar .

Usando o programa teste abaixo, a função apresentou erros.

Usando o debugger do MATLAB e o programa teste, identifique e corrija os erros da função .

O primeiro passo é passar a limpo os códigos do enunciado. Em um novo script, copie a função :

A função tem duas entradas e uma saída. A entrada deve ser um vetor com os coeficientes do polinômio e a entrada , o valor de com o qual calcularemos .

A saída é calculado para o valor .

Na linha 2, deseja-se criar um vetor de zeros por meio da função , de mesmo comprimento de . Este vetor se chama e armazenará os valores de para .

Na linha 3, deseja-se atualizar os valores de , calculando para .

Em outro script em branco, copie o programa teste e salve-o na mesma pasta onde você salvou a função :

Assim como fizemos para , vamos ver o que cada linha faz no programa teste. Na primeira linha, o comando limpa o Workspace do MATLAB cada vez que o programa é rodado. Como procuramos erros na função e teremos que chamá-la várias vezes para ver se corrigimos alguma coisa e encontrar mais erros, é importante limpar o Workspace a cada tentativa.

Na segunda linha, o comando limpa o Command Window do MATLAB cada vez que o programa é executado. Novamente, como vamos rodar o código diversas vezes, é importante limpar o Command Window a cada tentativa, para ficar mais fácil de ver qual erro foi corrigido e qual é o erro a ser corrigido na sequência, caso exista.

No programa teste, testamos em três casos diferentes, mas todos com o mesmo vetor de coeficientes de . Na linha 4, criamos o vetor contendo os coeficientes de .

Na linha 5, testamos para , chamando tendo como entrada e . Logo abaixo, imprimos o resultado de para no Command Window por meio do comando .

Na linha 7, testamos para , chamando tendo como entrada e . Novamente, na linha 8, imprimos o resultado de para no Command Window usando .

Na linha 9, cria-se um vetor que vai de a , com um passo de . Na linha 10, chamamos a função tendo como entrada e esse vetor .

Vamos executar o programa e ver qual o primeiro erro que o MATLAB encontra:

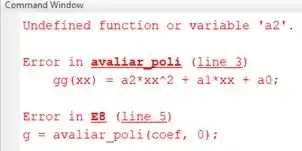
Ele nos diz que há um erro na linha 5 do programa teste, onde a função é chamada pela primeira vez. Este erro está em , na linha 3, e este erro é que a variável é desconhecida.

Se revermos o código de , vemos que as variáveis da linha 3, , ae , não foram definidas na função. Elas devem ser definidas a partir do vetor , que contém os coeficientes do polinômio. E repare: em nenhum momento em o vetor foi utilizado.

Para corrigir isto, inclua no começo da função os comandos:

Pois , como dito no enunciado. Desta forma, a função ficou com essa cara:

Execute o programa teste de novo para ver se corrigimos o erro:

O erro anterior sumiu, mas o MATLAB achou outro. Novamente, há um erro na linha 5 do programa teste, onde a função é chamada pela primeira vez. Este erro está em , na linha 7, e este erro é que é um vetor, e vetores não pode ter índices iguais a . Isto acontece pois na linha 7 temos e , logo, o MATLAB vai considerar e considerará um erro.

Para corrigir isso, simplesmente apague o do lado de na linha 7:

Rode o programa teste de novo para ver se finalmente conseguimos avançar além da linha 5 dele:

Opa, apareceram um e um ali, isso indica que o programa rodou direitinho até a linha 8 do programa do teste. O e o vieram do comando das linhas 6 e 8, pois a linha 6 mostra o resultado de e a linha 8, de .

Após imprimir o , o MATLAB nos diz que há um erro na linha 10 do programa teste, quando a função é chamada pela terceira vez, tendo como entrada e o vetor . Como é um vetor, o MATLAB não consegue criar o vetor de zeros na linha 6 de , pois a função só aceita números escalares como entrada.

Podemos corrigir esse erro pensando no que a linha 10 do programa faz. Na linha 10 do programa teste, queremos aplicar a função em um vetor , de forma a avaliar para vários valores de uma tacada só. Do jeito que está, ela só calcular se a entrada for um número, não um vetor.

Para isto, em , apague a linha que contém :

Após apagar o comando , na atual linha 6 de , onde é calculado, adicione um ponto à direita de em , de forma que a nova sintxe fica assim:

Isso faz com que, quando é um vetor, cada elemento dele seja elevado ao quadrado, de forma que a saída de também será um vetor. Essa operação não trará problemas quando for simplesmente um número, como podemos ver ao executar o programa após essa alteração:

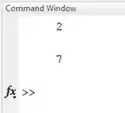
O programa roda normalmente, sem mensagens de erro. Se quiser, você pode ver o resultado da terceira aplicação de na linha 10 do programa teste, imprimindo no Command Window.

Pronto! Função corrigida! E gora ela funciona tanto para a entrada sendo um número escalar ou um vetor ;)