Analisando seu programa
Produzido por Gustavo BarbosaTeoria
Introdução
Olá, galerinha linda! Diga-me: você alguma vez na vida já planejou uma viagem, tipo um mochilão?
Um mochilão que vai durar umas duas semanas, em que você vai visitar várias cidades. Nestes mochilões, temos que programar tudo direitinho para aproveitar o máximo possível. Montar itinerário, reservar hostels, comprar passagens, etc. Por isso, normalmente a gente monta um esquema na nossa cabeça e fica repassando para ver se não esquecemos nada e termos uma viagem incrível!

Em programação, depurar ou debugar um código é um processo parecido. Debugamos um programa para encontrar erros, seja de sintaxe, digitação ou até lógica de programação mesmo, e os corrigirmos.
O MATLAB tem um debugger que ajuda muito neste processo, principalmente quando o código fica muito longo. É o debugger do MATLAB que vamos conhecer nesta aula =)
Criando breakpoints
Para vermos como usa o debugger do MATLAB, vamos direto para um exemplo. Crie um novo script no MATLAB e escreva o código abaixo. Vamos lá, eu te espero.

Pronto? O programa acima pede para o MATLAB criar um vetor com elementos. Os elementos de são números aleatórios, entre e . Em seguida, calcula-se a média dos elementos de (linha 4), que é armazenada na variável .
Nas linhas 4 e 5, são criados dois vetores para gerarmos o gráfico com os números randômicos: , que é um vetor que contém elementos iguais a ; e , que vai de a de um em um e servirá como o eixo do nosso gráfico. Aparentemente está tudo certo, né?
Vamos rodar a função:
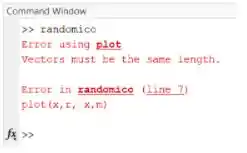
Vixe, deu errado. O MATLAB nos informa que tem um erro na linha 7 do programa, onde usamos a função .
“Ué”, você deve estar pensando, “mas não tem nada de errado com a linha 7 do código. E agora?”.
Repare que o MATLAB nos diz que o erro está relacionado ao tamanho dos vetores. Por isso, temos que ver o que está acontecendo antes da linha 7 do código, para ver de onde está vindo este problema com o comprimento dos vetores.
Para ver o que está acontecendo antes da linha 7, vamos usar um recurso chamado breakpoint.
Breakpoints são pontos no arquivo onde a execução do programa para temporariamente, para a gente avaliar o que vem antes deste ponto.
Criamos breakpoints no MATLAB na janela do Editor, naquela barra cinza à esquerda do código. Para criar um breakpoint, basta clicar nessa barra à esquerda, na linha onde você quer que o programa pare de rodar. No nosso exemplo, queremos ver o que acontece antes da linha 7, por isso vamos criar um breakpoint na linha 5:
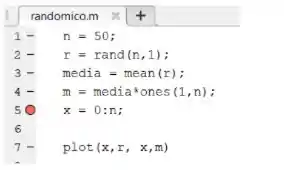
O breakpoint é a bolinha vermelha à esquerda da linha com o código .
Se mandamos rodar o programa, com a presença de pelo menos um breakpoint, o MATLAB entra no modo debugger e para de executar o programa na linha do breakpoint. A parada da execução é indicada por uma flechinha verde:

Neste momento, a execução está em “stand-by” e podemos verificar as variáveis acima da linha 5.
Verificando valores das variáveis
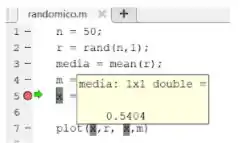
No modo debugger do MATLAB, podemos ver o que cada variável contém colocando o cursor do mouse em cima dela. Por exemplo, para conhecer o valor de , colocamos o cursor sobre ela e aparece um retângulo amarelo com seu tamanho, o tipo da variável e seu valor:
Já sabemos que nosso problema está no comprimento dos vetores. Vamos então dar uma checada neles fazendo o mesmo procedimento. Primeiro, vamos ver o vetor parando o cursor em cima da variável:

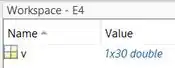
Ali diz que ele é um vetor .
Agora vamos ver o vetor :

Temos que o tamanho de é .
Resta ver o valor de . Como meu breakpoint está exatamente na linha que define , o vetor ainda não foi criado. Para criarmos ele, devemos executar a linha 5. Para isso, você pode clicar no botão “Step” no campo DEBUG acima do editor ou apertar F10.
Ao fazermos isso, a flechinha verde se desloca para baixo, indicando que a linha 5 foi executada:
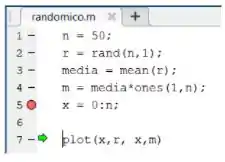
Vamos ver as informações do vetor :
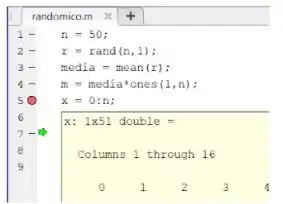
Xiiiiiiii, olha o tamanho dele: . Isso quer dizer que ele tem um elemento a mais do que e , por isso que nosso plot tá dando errado. Temos que reduzir o comprimento dele para o nosso programa rodar direito.
Antes de corrigirmos nosso código, vamos interromper o debugger. Clique no botão vermelho escrito “Quit Debugging” ou use o atalho Shift + F5.
Agora, vamos mudar a linha 5 para:
![]()
Indicamos ao MATLAB que queremos que o vetor comece em e não em . Desta forma, terá elementos e não mais . Você pode verificar mandando debugar de novo.
Antes de rodarmos o código de novo para vermos se dá certo, vamos deletar o breakpoint. Você pode apagá-lo clicando nele ou usado o atalho F12:
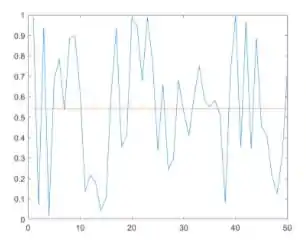
Hora da verdade! Bora rodar o programa! Com a alteração que fizemos, não temos mais o erro de comprimento de vetores e geramos este lindo gráfico:
Prontinho! Agora você conhece o básico do debugger do MATLAB. Conhecendo esses comandos básicos, já dá pra se virar bastante. Não esqueça de fazer os exercícios que preparei com muito carinho, para fixar o conteúdo ;D
Verificando valores das variáveis
Exercícios Resolvidos
Exercício Resolvido #1
“Adaptado de University of South Australia: MATLAB Practicals, de Kuva Jacobs e Yuliya Tugai. Debugging exercise, part 1, p. 17 (2013)”
O código abaixo cria um vetor que contém a raiz cúbica de todos os elementos de .

Descubra por que o programa não funciona, usando o MATLAB.
Passo 1
Este exercício pede que identifiquemos os erros do programa do enunciado, usando o MATLAB. Devemos copiar o programa em um novo script e rodá-lo algumas vezes, até que não apareçam mais mensagens de erro.
Passo 2
Crie um script novo no MATLAB e copie nele o programa do enunciado.
Antes de rodarmos o programa, vamos ver o que cada linha de código faz, para ajudar a identificar eventuais erros:

Na primeira linha, temos o comando . Este comando limpa o Workspace do MATLAB cada vez que o programa é rodado. Como procuramos erros no código e teremos que rodá-lo várias vezes para ver se corrigimos alguma coisa e encontrar mais erros, é importante limpar o Workspace a cada tentativa.
Na segunda linha, o comando limpa o Command Window do MATLAB cada vez que o programa é executado. Novamente, como vamos rodar o código diversas vezes, é importante limpar o Command Window a cada tentativa, para ficar mais fácil de ver qual erro foi corrigido e qual é o erro a ser corrigido na sequência, caso exista.
Na linha 4, criamos um vetor chamado de elementos.
Na linha 5, pegamos o vetor e elevamos a , para calcular a raiz cúbica de cada um dos seus elementos. O resultado dessa operação é armazenado em um vetor chamado , que contém a raiz cúbica de cada elemento de .
Passo 3
Agora que sabemos o que cada linha faz, vamos rodar nosso programa pela primeira vez.
Apareceu o seguinte erro no Command Window:

O MATLAB avisou que tem um erro na linha 5, dizendo que o operador só aceita como entrada um número escalar ou uma matriz quadrada. Isto quer dizer que o problema está em .
Passo 4
O MATLAB só consegue elevar a uma potência matrizes quadradas ou números escalares. é um vetor . Além disso, não queremos elevar o vetor a (ou seja, calcular a raiz cúbica de ), mas sim cada elemento de . Para fazermos isto, coloque um ponto ao lado de na linha 5:
![]()
Rode o programa novamente para ver se o programa foi corrigido. Dessa vez, nenhuma mensagem de erro deve aparecer. Para dar aquela conferida final, imprima no Command Window os vetores e , para ver se realmente cada elemento de é a raiz cúbica do elemento de que se encontra na mesma posição:

Tcharam! Descobrimos o problema do programa e o corrigimos ;D
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
“Adaptado de University of South Australia: ‘MATLAB Practicals’, de Kuva Jacobs e Yuliya Tugai (2013)”
Copie o programa abaixo em um script do MATLAB:

Descubra porque o programa não funciona, usando o debugger do MATLAB.
Passo 1
Este exercício pede que identifiquemos os erros do programa do enunciado, usando o debugger do MATLAB. Devemos copiar o programa em um novo script e rodá-lo algumas vezes, até que não apareçam mais mensagens de erro.
Passo 2
Crie um script novo no MATLAB e copie nele o programa do enunciado.
Antes de rodarmos o programa e procurarmos eventuais erros, vamos ver o que cada linha significa:

Na primeira linha, temos o comando . Este comando limpa o Workspace do MATLAB cada vez que o programa é rodado. Como procuramos erros no código e teremos que rodá-lo várias vezes para ver se corrigimos alguma coisa, é importante limpar o Workspace a cada tentativa.
Na segunda linha, o comando limpa o Command Window do MATLAB cada vez que o programa é executado. Novamente, como vamos rodar o código diversas vezes, é importante limpar o Command Window a cada tentativa, para ficar mais fácil de ver qual erro foi corrigido e qual é o erro a ser corrigido na sequência, caso exista.
Na linha 4, criamos uma variável chamada que armazena o número 9. Em seguida, criamos o vetor , que vai de 1 a , com um passo igual a 2.
Na linha 6, criamos o vetor , que inicia em 10 e termina em 1, com um passo de -1.
Finalmente, na linha 7, somamos os vetores e e armazenamos o resultado no vetor .
Agora que sabemos o que cada linha faz, vamos rodar nosso programa pela primeira vez.
Ooops, apareceu o seguinte erro no Command Window:

Temos um erro na linha em que os vetores e são somados (no meu script, o comando ficou na linha 7, pode ser que no seu script ele esteja em uma linha diferente, dependendo da forma que você copiou o programa). O MATLAB diz que as dimensões das matrizes não batem. Logo, deve ter alguma coisa na criação dos vetores e que fez com que eles tenham comprimentos diferentes, fazendo com que não consigamos somá-los.
Vamos encontrar essa coisa debugando o nosso programa.
Passo 3
Usamos breakpoints para debugar programas. Lembrando que um breakpoint é um ponto marcando uma linha de código, onde o programa vai parar temporariamente de ser executado, permitindo que a gente analise tudo o que aconteceu antes.
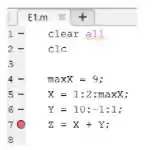
Como o erro está na linha 7, vamos criar um breakpoint nessa linha. Para isto, clique na barra cinza à esquerda do código, na linha 7 (ou na linha onde o MATLAB indicou que o erro aparece, caso você tenha copiado o programa um pouquinho diferente).
Vai aparecer um ponto vermelho onde você clicou, que é o nosso breakpoint:
Execute o programa novamente. O MATLAB entra em modo debugger e vai interromper a execução quando chegar na linha do breakpoint:
![]()
A interrupção é indicada pela flechinha verde, podemos ver tudo que tem acima dela. Como tivemos um problema de dimensões de matrizes, vamos dar uma olhada nos vetores e , para vermos os tamanhos deles. Para vermos os elementos e as dimensões dos vetores, devemos deixar o cursor do mouse sobre as variáveis.
Ao fazermos isso com o vetor , vemos que ele tem dimensões , isto é, ele tem 5 elementos:

Quando fazemos o mesmo com o vetor , vemos que ele tem dimensões :

Em outras palavras, tem o dobro de elementos de . É por isso que o MATLAB não consegue somar os dois.
Passo 4
Vamos tentar corrigir o problema. Antes, pare o debugger clicando em “Quit Debugging”:
Agora, precisamos encontrar uma forma de fazer com que os vetores e tenham o mesmo comprimento. Existem várias formas de fazer isso. Uma delas é mudarmos o valor de .
Pense comigo: se começa em 1 e tem passo 2, quanto deve ser para que tenha 10 elementos? O número de elementos de um vetor criado com o comando:
Pode ser calculado a partir da seguinte expressão:
Para o vetor :
Logo, a equação fica:
Temos que .
Vamos então trocar o valor de e debugar novamente para verificar como ficou o vetor :

Agora tem dimensões , assim como . Desta forma, conseguiremos somar os dois vetores sem problemas.
Passo 5
Vamos ver agora está tudo certo? Para executar a linha 7 no modo debugger, aperte F10 ou o botão step.
Quando você fizer isso, a flechinha verde vai descer uma linha de código, indicando que a linha 7 foi executada sem erros. Como a linha 7 é a última linha do programa, esta flechinha muda de orientação, apontando para baixo:
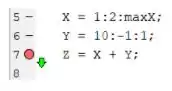
Note também que não apareceu nenhuma mensagem de erro no Command Window, apenas uma frase dizendo que o script acabou:
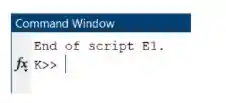
Logo, o MATLAB conseguiu somar os vetores e e armazenar a soma em , sem problemas.
Pronto! O programa está corrigido! Se quiser dar uma última verificada, apague o breakpoint clicando nele e mande o programa rodar novamente. Com as alterações feitas neste passo a passo, não deve aparecer nenhuma mensagem de erro.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
“Adaptado de University of South Australia: ‘MATLAB Practicals’, de Kuva Jacobs e Yuliya Tugai (2013)”
Copie o programa abaixo em um script do MATLAB:

O codigo acima plota a série:
Para inteiros de 1 a 100 e soma os primeiros 100 elementos da série. A soma dos 100 primeiros elementos desta série é aproximadamente 1,635.
Usando o debugger do MATLAB, corrija eventuais erros do código. Verifique ao final se a soma obtida corresponde a 1,635.
Passo 1
Este exercício pede que identifiquemos os erros do programa do enunciado, usando o debugger do MATLAB. Devemos copiar o programa em um novo script e rodá-lo algumas vezes, até que não apareçam mais mensagens de erro.
O programa plota a série , para inteiros de 1 a 100, e faz a soma dos 100 primeiros elementos. Ao final, devemos checar se o resultado da soma dá 1,635.
Quando o programa rodar sem problemas e o resultado bater, todos os erros do código foram corrigidos.
Passo 2
Crie um script novo no MATLAB e copie nele o programa do enunciado.
Antes de rodarmos o programa e procurarmos eventuais erros, vamos ver o que cada linha significa:

Na linha 1, temos o comando . Este comando limpa o Workspace do MATLAB cada vez que o programa é rodado. Como procuramos erros no código e teremos que rodá-lo várias vezes para ver se corrigimos alguma coisa, é importante limpar o Workspace a cada tentativa.
Na linha 2, o comando limpa o Command Window do MATLAB cada vez que o programa é executado. Novamente, como vamos rodar o código diversas vezes, é importante limpar o Command Window a cada tentativa, para ficar mais fácil de ver qual erro foi corrigido e qual é o erro a ser corrigido na sequência, caso exista.
Para criar todos os inteiros de 1 a 100 e podermos gerar a série , é criado o vetor na linha 4. O vetor vai de 1 a 100, a um passo de 1.
Em seguida, na linha 5, são criados os 100 primeiros elementos da série , a partir do vetor . Os 100 elementos são armazenados no vetor .
Na linha 6, é gerado o gráfico da série, por meio da função .
Finalmente, na linha 7, é feita a soma dos 100 primeiros elementos da série, por meio da função . A função soma os elementos do vetor de entrada, no caos aqui, o vetor .
Note que a linha 7 não termina com ponto e vírgula (;). Isso faz com que o resultado de apareça no Command Window sem nós termos que pedir.
Já sabemos o que acontece em cada linha do código, bora rodar nosso programa pela primeira vez!
Vixe, deu erro:
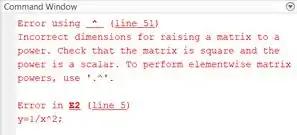
O MATLAB avisou que tem um erro na linha 5, dizendo que uma matriz não tem as dimensões corretas para ser elevada a uma potência. Isto quer dizer que o problema está em .
Passo 3
O MATLAB só consegue elevar a uma potência matrizes quadradas. Além disso, não queremos elevar o vetor ao quadrado, mas sim cada elemento de para criarmos a série. Para fazermos isto, coloque um ponto ao lado de na linha 5:
![]()
Bora ver se o problema foi corrigido? Rode o programa novamente. Deve ter aparecido a seguinte mensagem de erro:

O MATLAB nos diz que há um erro na linha 5 e que este erro está relacionado à operação de divisão. Ele diz que as dimensões das matrizes não batem.
Vamos criar um breakpoint na linha 5 para vermos o que está errado. Para criar um breakpoint, clique na barra cinza à esquerda do código, na linha 5 (ou na linha onde o MATLAB indicou que o erro aparece, caso você tenha copiado o programa um pouquinho diferente).
Vai aparecer um ponto vermelho onde você clicou, este é o breakpoint:
Execute o programa novamente. O MATLAB entra em modo debugger e vai interromper a execução quando chegar na linha do breakpoint:
![]()
Podemos ver os resultados das linhas de código que estão acima da flechinha verde. Vamos ver como é o vetor , colocando o cursor sobre ele:

O vetor tem dimensões . Não conseguimos fazer a divisão na linha 5 porque o que está no numerador é um número real.
Para conseguirmos fazer a divisão, acrescente um ponto ao lado do 1 na linha 5, como na imagem abaixo:
![]()
Passo 4
Vamos executar o programa novamente, para vermos se corrigimos o erro e se aparece algum outro. Antes disso, pare o debugger clicando em “Quit Debugging”:
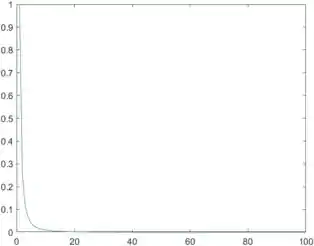
Rode o programa. Seguindo o passo a passo daqui, não é para ter mais nenhum erro. É para o seguinte gráfico ser gerado:
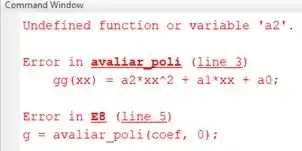
E o resultado da soma dos elementos de deve aparecer no Command Window:

Veja que é o mesmo valor dado no enunciado.
Pronto! O programa está corrigido!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
“Adaptado de University of South Australia: MATLAB Practicals, de Kuva Jacobs e Yuliya Tugai. Debugging exercise, part 3, p. 18 (2013)”
O código abaixo verifica o limite:
Calculando para . Em seguida, as posições dos elementos do vetor que armazena para cada valor de que estão dentro de uma dada tolerância, representada pela variável , são determinadas.

Descubra por que o programa não funciona, usando o MATLAB.
Passo 1
Este exercício pede que identifiquemos os erros do programa do enunciado, usando o MATLAB. Devemos copiar o programa em um novo script e rodá-lo algumas vezes, até que não apareçam mais mensagens de erro.
Passo 2
Em um novo script do MATLAB, copie o código do enunciado.
Antes de executarmos o programa, vamos ver o que cada linha de código faz, pois isso é necessário para identificar eventuais erros:

Na primeira linha, temos o comando , que limpa o Workspace do MATLAB cada vez que o programa é rodado. Como procuramos erros no código e teremos que rodá-lo várias vezes para ver se corrigimos alguma coisa e encontrar mais erros, é importante limpar o Workspace a cada tentativa.
Na segunda linha, o comando limpa o Command Window do MATLAB cada vez que o programa é executado. Novamente, como vamos rodar o código diversas vezes, é importante limpar o Command Window a cada tentativa, para ficar mais fácil de ver qual erro foi corrigido e qual é o erro a ser corrigido na sequência, caso exista.
Na linha 4, pedimos ao MATLAB para nos mostrar os números resultantes dos cálculos com 16 algarismos significativos.
Na linha 5, criamos um vetor , cujo primeiro elemento será , o segundo será , e assim sucessivamente, até o último elemento . Logo, . Isto é feito elevando-se a uma potência dada pelo vetor , que vai de a .
Na linha seguinte, calcula-se para cada elemento de , e os resultados são armazenados no vetor .
Na linha 8, calcula-se a tolerância, salva na variável . A tolerância é dada pela diferença entre e o oitavo elemento do vetor , que é muito próximo de .
A tolerância é usada na linha 9 para determinar qual elemento do vetor é maior ou igual a ela, por meio da função , que nos retorna os índices dos elementos de que sejam maiores ou iguais a . Desta forma, determina-se os elementos de que são o mais próximo possível de , considerando a tolerância adotada.
Passo 3
Após ver o que cada linha faz, vamos executar o programa pela primeira vez para identificar o primeiro erro. O Command Window fornecerá a seguinte mensagem:

O MATLAB avisou que tem um erro na linha 5, dizendo que o operador só aceita como entrada um número escalar ou uma matriz quadrada. Isto quer dizer que o problema está em .
O MATLAB só trabalha com potências que sejam números ou matrizes quadradas, e a potência na linha 5 é um vetor que vai de a . Queremos elevar a cada elemento do vetor . Para fazermos isto, coloque um ponto ao lado de na linha 5. Além disso, apague o ao final da linha, para quando executar o programa, o vetor ser impresso automaticamente no Command Window:
![]()
Vamos ver como ficou?

Agora está do jeito queremos e não há mais mensagens de erro. Contudo, isso não significa que está tudo certo ainda com o programa.
Passo 4
Vamos ver se está tudo certo com a linha 6, onde se deseja calcular para cada elemento de e gerar um vetor com os resultados. Se você imprimir no Command Window, você verá que ele é um escalar, e nos queremos que ele seja um vetor:

Para que seja um vetor com a solução de para cada elemento do vetor , devemos incluir um ponto à esquerda do sinal de divisão, na linha 6:
![]()
Vamos ver como ficou agora? Rode o programa e o imprima no Command Window:

Agora temos um vetor! E veja que legal: quando o elemento de é mais próximo de , o seu elemento de correspondente se aproxima de , como indica o limite .
Passo 5
Para finalizar, vamos ver qual o valor de :

E vamos ver as posições dos elementos de que são maiores ou iguais a :

Para ver quais elementos de estão nessas posições, digite no Command Window :

Podemos perceber que eles realmente são maiores que e muito próximos de .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
“Adaptado de Armstrong Atlantic State University – Engineering Studies – MATLAB Marina – Debugging Exercises. Exercício 4”
A função abaixo serve para avaliar o polinômio quadrático :

Onde é um vetor com os coeficientes do polinômio e é o valor de para o qual queremos avaliar .
Usando o programa teste abaixo, a função apresentou erros.

Usando o debugger do MATLAB e o programa teste, identifique e corrija os erros da função .
Passo 1
Neste exercício, vamos procurar erros na função rodando um programa teste.
Passo 2
O primeiro passo é passar a limpo os códigos do enunciado. Em um novo script, copie a função :

A função tem duas entradas e uma saída. A entrada deve ser um vetor com os coeficientes do polinômio e a entrada , o valor de com o qual calcularemos .
A saída é calculado para o valor .
Na linha 2, deseja-se criar um vetor de zeros por meio da função , de mesmo comprimento de . Este vetor se chama e armazenará os valores de para .
Na linha 3, deseja-se atualizar os valores de , calculando para .
Em outro script em branco, copie o programa teste e salve-o na mesma pasta onde você salvou a função :

Assim como fizemos para , vamos ver o que cada linha faz no programa teste. Na primeira linha, o comando limpa o Workspace do MATLAB cada vez que o programa é rodado. Como procuramos erros na função e teremos que chamá-la várias vezes para ver se corrigimos alguma coisa e encontrar mais erros, é importante limpar o Workspace a cada tentativa.
Na segunda linha, o comando limpa o Command Window do MATLAB cada vez que o programa é executado. Novamente, como vamos rodar o código diversas vezes, é importante limpar o Command Window a cada tentativa, para ficar mais fácil de ver qual erro foi corrigido e qual é o erro a ser corrigido na sequência, caso exista.
No programa teste, testamos em três casos diferentes, mas todos com o mesmo vetor de coeficientes de . Na linha 4, criamos o vetor contendo os coeficientes de .
Na linha 5, testamos para , chamando tendo como entrada e . Logo abaixo, imprimos o resultado de para no Command Window por meio do comando .
Na linha 7, testamos para , chamando tendo como entrada e . Novamente, na linha 8, imprimos o resultado de para no Command Window usando .
Na linha 9, cria-se um vetor que vai de a , com um passo de . Na linha 10, chamamos a função tendo como entrada e esse vetor .
Passo 3
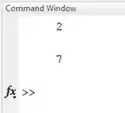
Vamos executar o programa e ver qual o primeiro erro que o MATLAB encontra:
Ele nos diz que há um erro na linha 5 do programa teste, onde a função é chamada pela primeira vez. Este erro está em , na linha 3, e este erro é que a variável é desconhecida.
Se revermos o código de , vemos que as variáveis da linha 3, , ae , não foram definidas na função. Elas devem ser definidas a partir do vetor , que contém os coeficientes do polinômio. E repare: em nenhum momento em o vetor foi utilizado.
Para corrigir isto, inclua no começo da função os comandos:

Pois , como dito no enunciado. Desta forma, a função ficou com essa cara:

Passo 4
Execute o programa teste de novo para ver se corrigimos o erro:

O erro anterior sumiu, mas o MATLAB achou outro. Novamente, há um erro na linha 5 do programa teste, onde a função é chamada pela primeira vez. Este erro está em , na linha 7, e este erro é que é um vetor, e vetores não pode ter índices iguais a . Isto acontece pois na linha 7 temos e , logo, o MATLAB vai considerar e considerará um erro.
Para corrigir isso, simplesmente apague o do lado de na linha 7:
![]()
Passo 5
Rode o programa teste de novo para ver se finalmente conseguimos avançar além da linha 5 dele:

Opa, apareceram um e um ali, isso indica que o programa rodou direitinho até a linha 8 do programa do teste. O e o vieram do comando das linhas 6 e 8, pois a linha 6 mostra o resultado de e a linha 8, de .
Após imprimir o , o MATLAB nos diz que há um erro na linha 10 do programa teste, quando a função é chamada pela terceira vez, tendo como entrada e o vetor . Como é um vetor, o MATLAB não consegue criar o vetor de zeros na linha 6 de , pois a função só aceita números escalares como entrada.
Podemos corrigir esse erro pensando no que a linha 10 do programa faz. Na linha 10 do programa teste, queremos aplicar a função em um vetor , de forma a avaliar para vários valores de uma tacada só. Do jeito que está, ela só calcular se a entrada for um número, não um vetor.
Para isto, em , apague a linha que contém :

Passo 6
Após apagar o comando , na atual linha 6 de , onde é calculado, adicione um ponto à direita de em , de forma que a nova sintxe fica assim:
![]()
Isso faz com que, quando é um vetor, cada elemento dele seja elevado ao quadrado, de forma que a saída de também será um vetor. Essa operação não trará problemas quando for simplesmente um número, como podemos ver ao executar o programa após essa alteração:
O programa roda normalmente, sem mensagens de erro. Se quiser, você pode ver o resultado da terceira aplicação de na linha 10 do programa teste, imprimindo no Command Window.
Pronto! Função corrigida! E gora ela funciona tanto para a entrada sendo um número escalar ou um vetor ;)
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
“Adaptado de Armstrong Atlantic State University – Engineering Studies – MATLAB Marina – Debugging Exercises”
Entre o programa abaixo no editor do MATLAB:

Lembre de adicionar os comandos e no começo do programa.
- Rode o programa e corrija os erros de sintaxe;
- Crie um breakpoint na linha: ;
- Debugue o programa avançando linha por linha do programa e observe o Workspace e o Command Window, procurando algum erro. Corrija os erros lógicos.
- Limpe o breakpoint da letra b e rode o programa corrigido, observando o Workspace e o Command Window.
Passo 1
O enunciado nos deu um código que contém alguns erros e pede para nos o corrigirmos. A intenção do código é mostrar cada elemento do vetor no Command Window.
Na letra a, é pedido para corrigirmos erros de sintaxe. Erros de sintaxe em programação são causados quando não seguimos as regras da linguagem que estamos utilizando, no nosso caso, o MATLAB. Os erros de sintaxe impedem a execução do programa.
A letra b pede para criarmos um breakpoint, para ajudar a responder a letra c. Na letra c, nos é pedido para corrigir erros lógicos. Em programação, erros lógicos não impedem a execução do programa. Eles levam a uma saída diferente da desejada e só podem ser detectados pelo programador ou pela programadora. O debugger do MATLAB nos ajuda a encontrar erros lógicos e a corrigi-los, por isso o usaremos para responder à letra c.
Finalmente, a letra d pede para tirarmos o breakpoint criado na letra b e para rodar o programa por completo.
Passo 2
Crie um script novo no MATLAB e copie o nele o programa do enunciado. Antes de rodarmos o programa e procurarmos eventuais erros, vamos ver o que cada linha significa e o que o programa faz, pelo menos na intenção:

Na linha 1, temos o comando . Este comando limpa o Workspace do MATLAB cada vez que o programa é rodado. Como procuramos erros no código e teremos que rodá-lo várias vezes para ver se corrigimos alguma coisa, é importante limpar o Workspace a cada tentativa.
Na linha 2, o comando limpa o Command Window do MATLAB cada vez que o programa é executado. Novamente, como vamos rodar o código diversas vezes, é importante limpar o Command Window a cada tentativa, para ficar mais fácil de ver qual erro foi corrigido e qual é o erro a ser corrigido na sequência, caso exista.
Na linha 4, criamos um vetor chamado , com 6 elementos.
Na linha 6, começamos um laço , com a intenção de mostrar no Command Window cada elemento de , um de cada vez.
A linha 7 imprime no Command Window o elemento da iteração corrente.
Finalmente, a linha 8 encerra o laço .
Resumindo, o programa deveria imprimir um elemento de a cada iteração do laço .
Agora que já sabemos qual é a intenção do programa, vamos rodá-lo para identificar problemas de sintaxe e resolver a letra a.
Ao tentarmos executar o programa, aparece a seguinte mensagem de erro:

Ela diz que há um erro de sintaxe na linha 6 do programa, no início do laço . Isto faz com que o programa nem seja executado.
Queremos que o MATLAB varra cada elemento de values usando o laço for. Para isto, devemos alterar a linha 6 para:
![]()
Na nova linha 6, criamos uma variável de controle , que vai de 1 até o número de elementos de , isto é, 6. O número de elementos de é dado pela função que dá o número de elementos de um vetor.
Rode o programa novamente. A saída no Command Window deve ter sido esta:
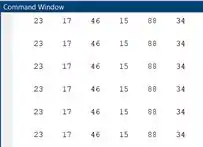
A correção que fizemos na linha 6 eliminou o erro de sintaxe e o MATLAB conseguiu rodar o programa. Portanto, a letra a está resolvida. Contudo, a saída não foi exatamente o que queríamos: o vetor foi impresso seis vezes, em vez de um elemento de ser impresso a cada iteração.
Passo 3
Para conseguirmos a saída que queremos, vamos começar pela letra b: criar um breakpoint na linha , isto é, na linha 7. Para criar o breakpoint, clique na barra cinza à esquerda do código, no Editor do MATLAB, na linha onde se deseja criá-lo:

Pronto, letra b feita :) Bora fazer a letra c.
Passo 4
A letra c pede para debugar o programa, avançando linha por linha. Enquanto executamos linha por linha, devemos observar o Workspace e o Command Window, para achar o erro no código.
Para ativar o modo debugger do MATLAB, mande rodar o programa. O programa vai ser executado até a linha 7, onde ele será interrompido. A linha onde o programa foi interrompido é indicada por uma flechinha verde:

Olhe o seu Workspace, ele deve estar assim:

Foi criada a variável de controle e ela por enquanto é igual a 1.
Vamos executar o programa linha por linha como o enunciado mandou. Para isso, aperte o botão “Step” ou use o atalho do teclado F10. Com isto, a flechinha verde desceu para a linha 8, indicando que a linha 7 foi executada:
![]()
A execução da linha 7 fez com que a função exibisse o vetor values no Command Window:
![]()
Vamos continuar avançando linha por linha. Aperte F10 novamente ou o botão “Step”. Como iniciamos um laço , a flechinha verde voltou para a linha 7.

Vamos ver novamente o Workspace:
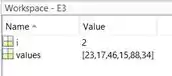
Repare que o valor de foi atualizado para 2, devido ao laço .
Aperte F10 novamente ou o botão “Step”. A linha 7 é executada novamente e o vetor é impresso no Command Window pela segunda vez:

Percebeu o padrão? Cada vez que avançamos uma iteração no laço , o valor de é atualizado e o vetor é impresso novamente. Como neste laço o vai de 1 a 6, após debugarmos, será igual a 6 e será impresso seis vezes no Command Window.
Isto está longe do que queremos, que é imprimir um elemento de a cada iteração do laço . Este é o erro lógico do programa.
Passo 5
Para corrigi-lo, altere a linha 7 para:

Em vez de , usamos , para indicar o elemento de que deve ser impresso. Por exemplo, no laço , inicialmente , logo, na primeira iteração, o comando da linha 7 será na prática . Isto fará com que o primeiro elemento do vetor , 23, seja impresso. Na iteração seguinte, e o comando da da linha 7 será na prática . Isto fará com que o número 17 seja impresso no Comand Window, pois ele é o segundo elemento de . Isto acontecerá para todos os elementos de até .
Vamos visualizar este processo debugando. Repare que nem tinha apagado ainda o nosso breakpoint.
Rode o programa novamente para o MATLAB entrar em modo debugger:

Vamos ver o Workspace:

Temos . Vamos apertar F10 ou o botão “Step” para executar a linha 7. Ao fazermos isso, o Command Window imprime :
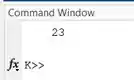
Note que é o primeiro elemento de e ele foi impresso na primeira iteração do laço .
Aperte F10 novamente ou o botão “Step” e repare no valor de no Workspace:
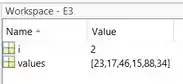
Temos . Ao executarmos a linha 7 novamente, o Command Window imprime :
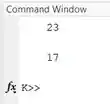
Que é o segundo elemento de , impresso na segunda iteração.
Percebeu a diferença entre e ? Ao incluirmos o , um elemento de é impresso a cada iteração do laço . Sem o , o vetor inteiro é impresso a cada iteração.
Após terminar de debugar, executando linha por linha, o resultado será todos os elementos de impressos no Command Window, sendo que um elemento é impresso por vez:

No Workspace, estará igual 6:
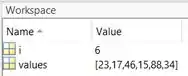
O erro lógico está corrigido, portanto, a letra c está respondida.
Passo 6
A letra d para eliminar o breakpoint e rodar o programa normalmente. Ela pede também para ver o Command Window e o Workspace.
Apague o breakpoint clicando nele e rode o programa. O seu Command Window deve ter ficado assim:

E o Workspace, assim:
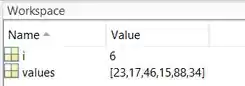
Eles estão da mesma forma que ficaram ao terminarmos de debugar. Isto ocorre pois não pedimos ao MATLAB para executar e avaliar linha por linha nosso código, nós pedimos para o MATLAB executá-lo de uma vez, chegando diretamente ao resultado final.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
“Adaptado de Armstrong Atlantic State University – Engineering Studies – MATLAB Marina – Debugging Exercises”
Entre o programa abaixo no editor do MATLAB:

Lembre de adicionar os comandos e no começo do programa.
- Rode o programa e corrija os erros de sintaxe;
- Crie dois breakpoints, nas linhas:
- Debugue o programa avançando linha por linha do programa e observando o Workspace e o Command Window, procurando algum erro. Corrija os erros lógicos.
- Limpe os breakpoints da letra b e rode o programa corrigido.
Passo 1
O enunciado nos deu um código que contém alguns erros e pede para nós o corrigirmos. A intenção do código é gerar um vetor de 30 elementos e somar somente os elementos positivos. Mas calma que eu já vou explicar isso em detalhes no próximo passo. Vamos entender o que o enunciado quer primeiro.
Na letra a, é pedido para corrigirmos erros de sintaxe. Erros de sintaxe em programação são erros causados quando não seguimos as regras da linguagem que estamos utilizando, no nosso caso, o MATLAB. Os erros de sintaxe impedem a execução do programa.
A letra b pede para criarmos dois breakpoints, para ajudar a responder a letra c. Na letra c, nos é pedido para corrigir erros lógicos. Em programação, erros lógicos não impedem a execução do programa. Eles levam a uma saída diferente da desejada e só podem ser detectados pelo programador ou pela programadora. O debugger do MATLAB nos ajuda a encontrar erros lógicos e a corrigi-los, por isso o usaremos para responder à letra c.
Finalmente, a letra d pede para tirarmos os breakpoints criados na letra b e para rodar o programa por completo.
Passo 2
Crie um script novo no MATLAB e copie nele o programa do enunciado. Antes de rodarmos o programa e procurarmos eventuais erros, vamos ver o que cada linha significa e o que o programa faz (ou o que deveria fazer):

Na linha 1, temos o comando . Este comando limpa o Workspace do MATLAB cada vez que o programa é rodado. Como procuramos erros no código e teremos que rodá-lo várias vezes para ver se corrigimos alguma coisa, é importante limpar o Workspace a cada tentativa.
Na linha 2, o comando limpa o Command Window do MATLAB cada vez que o programa é executado. Novamente, como vamos rodar o código diversas vezes, é importante limpar o Command Window a cada tentativa, para ficar mais fácil de ver qual erro foi corrigido e qual é o erro a ser corrigido na sequência, caso exista.
Na linha 4, criamos um vetor chamado , que contém 30 números inteiros entre -10 e 100, gerados de forma aleatória. O vetor é criado usando duas funções do MATLAB: e . A função serve para gerar números reais aleatórios, dentro do intervalo [0,1]. Já a função serve para arredondar números quebrados para o inteiro mais próximo.
Vamos ver como é a estrutura de cada uma destas duas funções. A função tem a seguinte estrutura:
Ela retorna uma matriz com e , composta por números aleatórios, que vão de 0 a 1.
A função tem o formato:
Ela arredonda cada elemento de para o inteiro mais próximo.
Logo, na linha 4, o vetor é criado seguindo estas etapas:
- A primeira parte da linha que é executada é , que gera um vetor com 30 elementos aleatórios, entre 0 e 1. O vetor resultante é multiplicado por 110. Assim passamos a ter 30 elementos variando entre 0 e 110;
- Em seguida, -10 é somado ao vetor resultante. Isto é feito para que os elementos de no final tenham um valor entre -10 e 100;
- Finalmente, cada elemento do vetor gerado na etapa acima é arredondado para o inteiro mais próximo, por meio da função .
Na linha 6, iniciamos um laço , para varrer cada elemento do vetor . É criada uma variável de controle , que vai de 1 até o número de elementos de , isto é, 30, com um passo de 1. O número de elementos de é dado pela função que retorna a quantidade de elementos de um vetor.
Na linha 7, criamos uma condição para avaliar cada elemento de , verificando se ele é maior ou igual a 0, isto é, positivo. Fazemos isso para pegarmos somente elementos de que sejam positivos, para fazer a soma na linha seguinte.
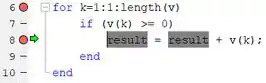
A linha 8 adiciona um elemento positivo de , a cada iteração, à soma obtida na iteração anterior.
A linha 9 encerra a condição da linha 7 e a linha 10 encerra o laço .
A linha 12 apresenta no Command Window do MATLAB a soma dos elementos positivos de .
Agora que sabemos o que cada linha significa, vamos executar o programa para encontrar os erros de sintaxe e resolver a letra a do exercício.
Ao rodarmos o programa, aparece a seguinte mensagem no Command Window:
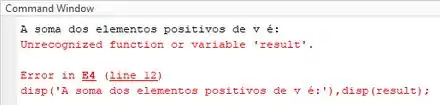
Note que apareceu a string dentro do comando da linha 12. Isso quer dizer que não há erros de sintaxe, já que o programa foi executado.
Contudo, há outros erros. Veja que o MATLAB indicou que há um erro na linha 12: ele não reconheceu a variável . Isso quer dizer que a linha 8 não foi executada. Para encontrarmos a fonte do problema, devemos debugar nosso programa.
Passo 3
Para começarmos a debugar, precisamos criar breakpoints, para o MATLAB entrar em modo debugger. Por isso, neste passo vamos responder a letra b do exercício.
Na letra b, é pedido para criar dois breakpoints, nas linhas:
Que são as linhas 6 e 8 do programa. Para criar os breakpoints, clique na barra cinza à esquerda do código, na janela do Editor do MATLAB, nas linhas onde queremos que a execução programa seja interrompida temporariamente. Aparecerão duas bolas vermelhas:
Essas duas bolas vermelhas são os breakpoints.
Pronto, a letra b do exercício está feita ;)
Passo 4
Com os breakpoints criados, podemos debugar o programa e fazer a letra c do exercício. A letra c pede para executar o programa linha por linha e, enquanto executamos, devemos observar o Workspace e o Command Window, para achar o erro no código.
Para ativar o modo debugger do MATLAB, mande rodar o programa. O programa vai ser executado até a linha 6, onde ele será interrompido. A linha onde o programa foi interrompido é indicada por uma flechinha verde:

Olhando o Workspace, vemos que a variável foi criada sem problemas:
Vamos executar o programa linha por linha como o enunciado mandou. Para isso, aperte o botão “Step” ou use o atalho do teclado F10. Com isto, a flechinha verde desceu para a linha 7, indicando que a linha 6 foi executada:

Observe o Workspace: a variável de controle foi criada e é igual a 1.

Vamos executar outra linha novamente. Aperte F10 ou botão “Step”. Ao fazer isso, a flechinha pulou da linha 7 para a linha 9, indicando que a condição do não foi respeitada:

Continue executando linha por linha, até atingir as 30 iterações. Você vai perceber que em nenhum momento a condição será respeitada, fazendo com que a variável não seja criada nem atualizada.
Isto acontece devido à forma como a condição do da linha 7 foi escrita: nela, o vetor inteiro foi avaliado, e não somente um elemento dele. O que a gente queria era analisar os 30 elementos do vetor (procurando pelos positivos) e foi por isso que criamos um loop. Mas estamos fazendo outra coisa. Estamos analisando 30 vezes se o vetor inteiro é positivo.
Um vetor é positivo se todos os seus elementos são positivos. E, como é muito provável que o vetor tenha pelo menos um elemento negativo, avaliando ele no todo, a condição será sempre falsa e a linha 8 não será executada em momento algum. Encontramos aqui o primeiro erro lógico do programa.
Interrompa o debugger clicando em “Quit debugging” para corrigirmos o erro da linha 7.
Passo 5
Para corrigir o erro lógico da linha 7, adicione à direita da , na condição do , como na imagem abaixo:

Fazendo isso, um elemento de será avaliado por vez na linha 7. Quando o laço for iniciar, e a linha 7 vai avaliar , que é o primeiro elemento de . Na segunda iteração, e será avaliado na condição do , e assim sucessivamente. A cada iteração o elemento , que ocupa a posição , é avaliado.
Note que na linha 8 também temos um vetor , que está sendo somado a . Novamente temos o vetor inteiro, onde deveria ser apenas um dos seus elementos. Como queremos que seja somado um elemento positivo por vez, vamos colocar um à direita de nesta linha também:

Bora ver o que acontece se executarmos o programa de novo? Ele vai ser interrompido novamente na linha 6, por causa do breakpoint. Execute a linha 6 apertando F10 ou o botão “Step”, para irmos para a linha 7 e execute esta linha em seguida. Perceba que agora conseguimos entrar no bloco do :
Como é a primeira iteração, , e a condição do foi atendida, isto quer dizer que o primeiro elemento de é positivo. Como conseguimos entrar pelo menos uma vez no bloco e atingir a linha 8, isto significa que corrigimos o primeiro erro de lógica. Ufa! Então vamos continuar!
Passo 6
Execute a linha 8 apertando F10 ou “Step”. Aparecerá a seguinte mensagem de erro no Command Window:
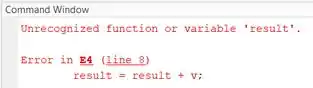
O MATLAB nos avisa que há um erro na linha 8: ele não reconheceu a variável . Isto porque ela não foi definida antes da linha 8.
Para corrigirmos o erro, interrompa o debugger, crie a variável na linha acima do laço e diga que ela é igual a 0:

A variável representa a soma dos elementos positivos de . Ela começará no programa como e será atualizada a cada iteração do laço , quando a linha 8 for executada. Ela receberá ela mesma somada com o elemento de da iteração corrente. Desta forma, quando o laço estiver concluído, terá a soma de todos os elementos positivos de .
Vamos testar novamente. Rode o programa para o MATLAB entrar em modo debugger e execute uma linha por vez até que a linha 8 seja atingida. Com a alteração que fizemos, não aparecerá mais o erro, pois a variável foi definida. Continue executando o código linha por linha e você verá que a variável muda a cada iteração.
Passo 7
Continue executando o programa linha por linha até o final. Quando o laço terminar, a linha 12 do código é executada e a variável é impressa no Command Window:

Lembre que a sua variável com certeza vai ser diferente da minha, pois é criado de forma aleatória.
Como chegamos até o final do programa sem erros, o programa foi corrigido e podemos fazer a letra d do exercício.
Passo 8
A letra d do exercício pede para apagar os breakpoints e rodar o programa. Para apagá-los, clique neles e eles desaparecerão. Ou clique em “Breakpoints” -> “Clear all”:

Isto também fará com que todos os breakpoints sumam.
Executando o programa, temos o seguinte resultado no Command Window:

Note que ele é diferente do passo anterior, pois é criado de forma aleatória.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
“Adaptado de Armstrong Atlantic State University – Engineering Studies – MATLAB Marina – Debugging Exercises”
Entre o programa abaixo no editor do MATLAB:

O programa pede ao usuário informar o número de transações a serem efetuadas. Em seguida, ele lê a entrada, em reais, de cada transação e controla o valor total das transações. Ao final, ele apresenta a soma, em reais, dos valores de cada transação.
Crie breakpoints onde achar necessário e debugue o programa, corrigindo erros de sintaxe e de lógica.
Passo 1
O enunciado nos passou um código que intencionalmente tem erros e nos pede para corrigi-lo. Existem no programa erros de sintaxe e de lógica.
Erros de sintaxe em programação são erros causados quando não seguimos as regras da linguagem que estamos utilizando, no nosso caso, o MATLAB. Os erros de sintaxe impedem a execução do programa.
Em programação, erros lógicos não impedem a execução do programa. Eles levam a uma saída diferente da desejada (às vezes incorreta) e só podem ser detectados pelo programador ou pela programadora. O debugger do MATLAB nos ajuda a encontrar erros lógicos e a corrigi-los, por isso nos é pedido para criar breakpoints e para debugar o programa.
Passo 2
Crie um script novo no MATLAB e copie o nele o programa do enunciado. O enunciado nos informou o que este programa deve fazer: ele pede para o usuário entrar com o número de transações que ele deseja fazer, para pedir, em seguida, o valor de cada transação. O programa controla o valor total das transações e informa ao final o valor total das transações.
Antes de rodarmos o programa e procurarmos eventuais erros, vamos ver o que cada linha significa para ver o que o programa faz para atingir seu objetivo:

Na linha 1, temos o comando . Este comando limpa o Workspace do MATLAB cada vez que o programa é rodado. Como procuramos erros no código e teremos que rodá-lo várias vezes para ver se corrigimos alguma coisa, é importante limpar o Workspace a cada tentativa.
Na linha 2, o comando limpa o Command Window do MATLAB cada vez que o programa é executado. Novamente, como vamos rodar o código diversas vezes, é importante limpar o Command Window a cada tentativa, para ficar mais fácil de ver qual erro foi corrigido e qual é o erro a ser corrigido na sequência, caso exista.
Uma variável chamada é criada na linha 4 e ela é igual a .
Na linha 5, pedimos ao usuário para informar o número de transações, por meio do comando . O número de transações é armazenado em .
Na linha 7, se inicia um laço . O bloco do laço é executado enquanto a condição for verdadeira. é uma variável de controle que conta quantas vezes o bloco do foi executado, isto é, conta o número de iterações.
Na linha 8, é pedido ao usuário para informar o valor de uma transação, também usando o comando . O valor da transação é armazenado na variável .
Na linha 9, o valor total das transações é atualizado, utilizando a variável criada na linha 4. A variável é atualizada considerando o valor informado pelo usuário na linha 8.
Na linha 10, a variável de controle é atualizada, adionando ao valor que tinha na iteração anterior.
A linha 11 indica que o bloco do se encerra ali.
A linha 13 imprime no Command Window o resultado da soma das transações, usando a função .
Agora que já sabemos o que cada linha faz, vamos rodar o programa pela primeira vez. Apaecerá no Command Window a seguinte mensagem:
![]()
O MATLAB exibiu a string do comando da linha 5, indicando que o programa foi executado. Isto significa que o programa não possui erros de sintaxe, já que o MATLAB conseguiu rodá-lo.
Passo 3
Vamos informar um número de transações para o programa continuar rodando, para vermos se não identificamos algum erro. Vou dizer que quero fazer duas transações, entrando o valor no Command Window. Desta forma, fica mais fácil de eu verificar se o resultado final estará certo.
Ao entrar o valor no Command Window, aparece a seguinte mensagem de erro:

O MATLAB nos informa que há um erro na linha 7, onde se inicia o . Ele não reconheceu a variável . Se olharmos o código atentamente de novo, percebemos que a variável não foi definida antes da linha 7 e é por isso que o MATLAB não a reconhece.
Para corrigirmos este erro, vamos definir a variável na linha 6 e dizer que ela é igual a :

Fizemos antes de iniciar o laço porque ele serve para contar quantas vezes o bloco foi executado. Perceba que na primeira iteração do while, vai ficar igual a ao passarmos pela linha 10, que diz que . Na segunda iteração, vai se transformar em pois a execução da linha 10 adicionar ao valor de da iteração anterior. Esse processo acontece a cada iteração do .
Passo 4
Vamos rodar o programa novamente para ver se achamos outro erro. Vamos informar novamente que queremos fazer transações, isto é, .

A mensagem de erro do passo anterior não aparece mais. O MATLAB nos pede o valor da transação, indicando que a linha 8 do código foi executada normalmente. Vamos dizer que queremos fazer uma transação de :

O MATLAB nos pede novamente para informar um valor de transação, já que pedimos para fazer duas transações. Vamos dizer que queremos fazer mais uma transação de :

Perceba que já há indícios que temos algum erro de lógica no código: o MATLAB pediu para entrarmos um terceiro valor de transação, sendo que nós dissemos que queríamos fazer somente duas transações. Vamos interromper a execução do código usando o atalho do teclado e criar um breakpoint para debugar o programa.
Crie um breakpoint na linha 10, onde a variável é atualizada, clicando na barra cinza à esquerda do código, no Editor do MATLAB:

A bolinha vermelha que apareceu é o brekpoint que definimos. Vamos rodar o programa novamente e ativar o modo debugger do MATLAB. O programa é executado até a linha 9 e é interrompido na linha 10:

Note que eu informer novamente que queremos fazer duas transações e já informei que a primeira transação é de . Na janela do Editor, apareceu uma flechinha verde na linha onde foi criado o breakpoint, indicando a interrupção do programa:

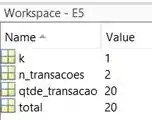
Antes de executar o programa linha por linha para identificarmos o erro, vamos ver como está nosso Workspace:
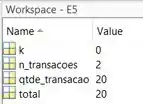
Perceba que, por enquanto, . Vamos executar a linha 10, usando o atalho do teclado F10 ou apertando o botão “Step”. Em seguida, olhe o Workspace novamente:
Agora, . Perceba que , por isso o bloco do será executado novamente. Continue executando o programa linha por linha até chegar na linha 10 novamente. Neste momento, seu Command Window estará assim:

O MATLAB nos pediu para informar o valor da segunda transação, novamente eu disse que quero fazer uma transação de . Vamos ver como está o Workspace:
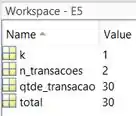
ainda não foi atualizado e continua igual a porque ainda não executamos a linha 10. Ao fazermos isto, ele se tornará igual a :
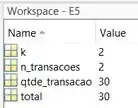
Note que, neste momento, e se continuarmos executando o programa linha por linha, o bloco será rodado novamente, pois a condição dele é .
Contudo, não queremos que o bloco seja executado mais uma vez, pois isso significa que estaremos fazendo uma terceira transação, sendo que só queremos fazer duas.
Aqui percebemos um erro de lógica no código: o laço não pode ser executado quando , para não fazermos uma transação a mais do que a gente pediu. Para corrigirmos este erro, interrompa o debugger apertando o botão “Quit debugging” e mude a condição do na linha 7 para :

Desta forma, o bloco do não será executado quando .
Vamos testar novamente? Apague o breakpoint da linha 10, clicando nele, rode o programa e peça para fazer duas transações, uma de e outra de .
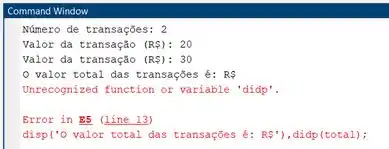
O seu Command Window deve ter ficado assim. Perceba que o problema de o MATLAB fazer uma transação a mais do que o pedido foi corrigido, pois ele pediu para informarmos o valor de uma transação duas vezes. Contudo, apareceu outra mensagem de erro, que diz que há um erro na linha 13.
Passo 5
A mensagem de erro diz que o MATLAB não reconheceu a variável ou função na linha 13. Se olharmos para o teclado de nossos computadores, descobrimos este erro se trata de um erro de digitação: quem escreveu o programa queria ter digitado em vez de , mas acabou apertando a tecla em vez da , que estão lado a lado no teclado.
Na linha 13, substitua por e rode o programa novamente, para vermos se não há mais algum erro. Novamente, vamos entrar com e pedir que a primeira transação seja de e a segunda, de . Seu Command Window deve ter ficado assim:

Oba! Nenhuma mensagem de erro! O programa foi executado até o final sem problemas!
Pera, mas viu o valor total das transações que o MATLAB nos informou? Ele disse que o valor total das transações é de , mas deveria ser de , não? Isto quer dizer que ainda há um erro lógico em nosso programa.
Passo 6
É na linha 13 que o valor total das transações é impresso no Command Window:
![]()
Veja que ela imprime primeiro uma string e, em seguida, a variável , que representa a soma de todas as transações.
Para identificar o erro, vamos ver o valor que assumiu ao final do programa:
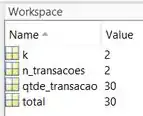
Perceba que está igual à , qua assumiu ao final do programa o valor de . Contudo, deveria ser a soma da primeira e da segunda transação, logo, deveria ser igual a no final do programa.
O problema deve estar na linha 9, onde a variável é atualizada dentro do bloco . Vamos criar um breakpoint na linha 9 para vermos como a variável total está sendo atualizada. Para isto, clique na barra cinza à esquerda do código, na janela Editor do MATLAB, sobre a linha 9. O breakpoint aparece representado pela bolinha vermelha.

Vamos debugar o programa novamente. Rode-o e diga quer quer fazer duas transações novamente, sendo que a primeira é de . A execução do programa será interrompida na linha 9 e seu Command Window estará assim:

Vamos ver o Workspace? Por enquanto, pois a variável ainda não foi atualizada:

Vamos agora rodar o programa linha por linha. Execute a linha 9 apertando F10 ou o botão “Step” e veja o valor que assumiu no Workspace:
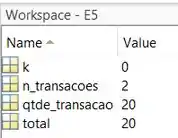
Agora, , que é igual ao valor da primeira transação que fizemos, que foi armazenado na variável . Por enquanto, está tudo certo.
Continue a executar o programa linha por linha, até atingir a linha 9 novamente. Não a execute ainda. Durante este processo, o MATLAB vai pedir o valor da segunda transação, de . Seu Command Window deve estar assim:

Vamos ver o Workspace:
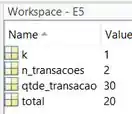
A variável foi atualizada para e a variável ainda não foi atualizada. Vamos executar a linha 9 e observar o Workspace:
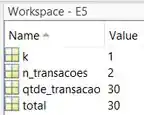
O ficou igual a , em vez de somar ao valor da primeira transação isto é, . Temos um problema no cálculo da atualização da variável .
Note que na linha 9, é atualizado pelo comando:
![]()
Que diz que é igual a . Mas não é isso que queremos, queremos que armazene a soma das transações. Para que isso seja feito, altere a linha 9 para:
![]()
Desta forma, é atualizada ao somar o valor que tinha na iteração anterior com o valor que a variável acabou de assumir.
Vamos ver se funcionou? Apague o breakpoint e rode o programa novamente.
Passo 7
De novo, diga que quer fazer duas transações, a primeira de e a segunda de . Seu Command Window deve estar assim:

Agora a soma dos valores das transações está correto: . Se olharmos o Wokspace, veremos que está diferente de e que :

Pronto! Programa corrigido! Se quiser, pode fazer mais alguns testes, mudando o número de transações e os valores das transações. Com as correções que fizemos, o programa vai rodar sem problemas.
Resposta
Ei, a resposta está no passo a passo :)