Determine as reações de apoio do pórtico abaixo, sabendo que o mesmo sofre um recalque vertical para baixo de 5cm no apoio A. E no apoio B, ainda sofre um recalque de 10 cm pra cima e 3 cm para direita.
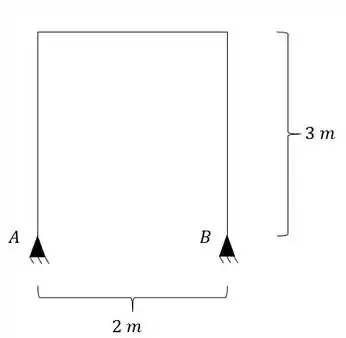
Passo 1
Sabemos que a primeira coisa que devemos fazer é determinar o número de hiperestáticos.
- Hiperestáticos totais pelo macete
- Sabemos que temos 2 apoios do segundo gênero, totalizando 4 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
Ou seja, nossa estrutura possui um grau de hiperestaticidade, que se eu conseguir tirar da nossa estrutura, transforma a nossa estrutura em isostática.
Quebrando um vinculo teremos a seguinte nova estrutura.
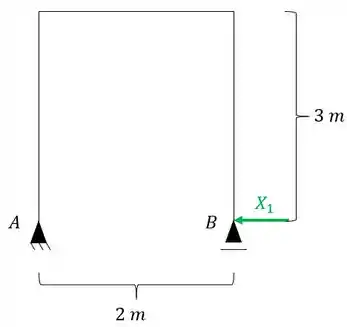
E até aqui a gente sabe resolver de boas, o que aparece de novo é o seguinte.
Pra determinar a deformação no sistema zero, que nesse caso é um recalque de apoio, precisamos obrigatoriamente colocar uma carga unitária no mesmo lugar, na mesma direção e no mesmo sentido do hiperestático, porém iremos calcular a deformação de maneira DIFERENTE do que fazemos com o hiperestático.
Apesar da carga estar na mesma posição e sentido do hiperestático, para o hiperestático iremos calcular o diagrama de momentos, porém para o sistema zero iremos calcular as deformações de recalque. Parece meio embolado, mas é bem tranquilo, me segue aqui.
Passo 2
Como eu disse, no sistema zero colocamos uma carga unitária na mesma posição, direção e sentido do hiperestático, com isso teremos.
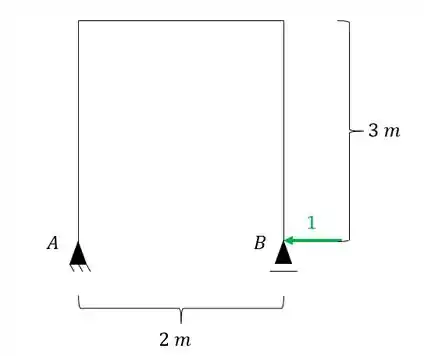
Para esse sistema como definimos a deformação quando estamos vendo o recalque? Não seria exatamente calculando as reações de apoio, e usando a nossa formulazinha?
Determinando as reações de apoio desse sistema teremos que:
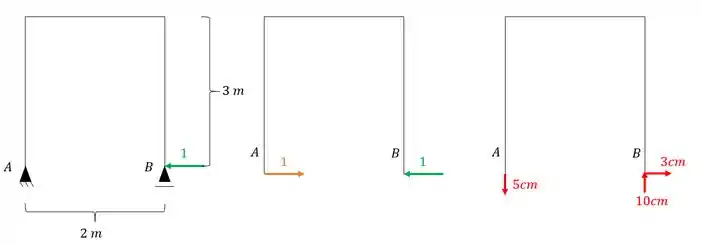
E como eu disse, precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
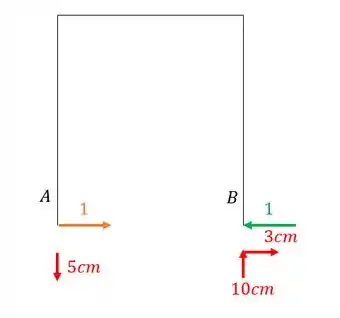
Como o 4cm não tem par, só iremos ter dois termos.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,

e sempre que for no sentido contrário, será negativa.

Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
Sabe quem é essa deformação? É exatamente o nosso , então podemos escrever ele como.
Passo 3
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
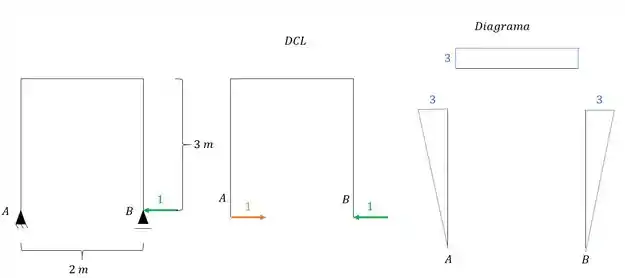
E para determinar faremos
Como , teremos que
E assim teremos que o nosso sistema será:
Substituindo teremos que
Como só tivemos reações horizontais sabemos que as reações serão dadas por:

Resposta
Reações horizontais de apoio
