Aplicação método das forças –Recalque
Produzido por Pablo RicardoTeoria
Introdução
Para cálculo dos esforços devido ao recalque, basta pensarmos que na verdade, os recalques são os carregamentos do sistema zero. E ai que entra a jogada: no sistema zero, temos uma estrutura isostática carregada com recalque de apoio, e nesse caso, sabemos que em estruturas isostáticas, obrigatoriamente, os digramas de momento, cortante e normal devido ao recalque são zero, o que facilita a nossa conta.
Algo que também é importante é que se você estiver em uma questão com itens a) , b) e c) em que no item a) você avalie um carregamento, no b) a temperatura e no c) o recalque, você não precisara calcular tudo de novo, aqui em baixo eu vou dar esse resuminho:
- As deformações , e você vai ter que calcular em cada item, tanto na a) quanto no b) quanto no c)
- As deformações , , todos esses você só calcula uma vez, ou seja, ao fazer o item a) você já determinou o sistema que será usado no b) e no c) , faltando definir, é claro, somente o que definimos aqui em cima.
Em resumo, se nosso sistema for
Onde e serão definidos em cada um dos itens (a, b e c). E e serão as incógnitas de cada um dos itens, então também vão ser definidos dependendo se estamos no a, b ou c. Porém tudo que está em preto será determinado apenas uma vez.
Entendida essa introdução, vamos ver como aplicar ao nosso problema ao recalque.
Recalque
Suponho que na estrutura hiperestática abaixo queremos saber as reações de apoio quando a estrutura sofre um recalque vertical de 2cm para baixo no apoio da direita, e sofre um recalque horizontal de 5 cm para esquerda no apoio da esquerda.
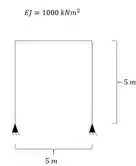
Sabemos que a primeira coisa que devemos fazer é determinar o número de hiperestáticos.
- Hiperestáticos totais pelo macete
- Sabemos que temos 2 apoios do segundo gênero, totalizando 4 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
Ou seja, nossa estrutura possui um grau de hiperestaticidade, que se eu conseguir tirar da nossa estrutura, transforma a nossa estrutura em isostática.
Quebrando um vinculo teremos a seguinte nova estrutura.
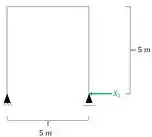
E até aqui a gente sabe resolver de boas, o que aparece de novo é o seguinte.
Pra determinar a deformação no sistema zero, que nesse caso é um recalque de apoio, precisamos obrigatoriamente colocar uma carga unitária no mesmo lugar, na mesma direção e no mesmo sentido do hiperestático, porém iremos calcular a deformação de maneira DIFERENTE do que fazemos com o hiperestático.
Apesar da carga estar na mesma posição e sentido do hiperestático, para o hiperestático iremos calcular o diagrama de momentos, porém para o sistema zero iremos calcular as deformações de recalque. Parece meio embolado, mas é bem tranquilo, me segue aqui.
Sistema zero
Como eu disse, no sistema zero colocamos uma carga unitária na mesma posição, direção e sentido do hiperestático, com isso teremos.
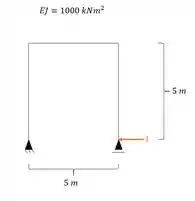
Para esse sistema como definimos a deformação quando estamos vendo o recalque? Não seria exatamente calculando as reações de apoio, e usando a o nossa formulazinha?
Determinando as reações de apoio e as deformações que foram dadas no enunciado como:
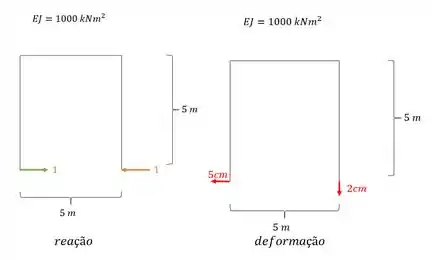
E como eu disse, precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
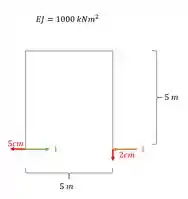
Como o 2cm não tem par, só iremos ter um termo.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva, e sempre que for no sentido contrário, será negativa.
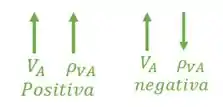
Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
Sabe quem é essa deformação? É exatamente o nosso , então podemos escrever ele como.
Sistema 1
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
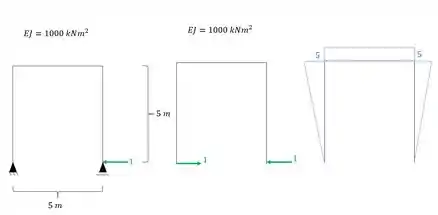
E para determinar faremos
E assim teremos que o nosso sistema será:
Substituindo teremos que
E assim conseguimos determinar todos os outros esforços da estrutura com o valor de .
E é isso, partiu fazer uns exercícios?
Recalque
Sistema zero
Sistema 1
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Determine as reações de apoio do pórtico abaixo, sabendo que o apoio sofre um recalque de para baixo.
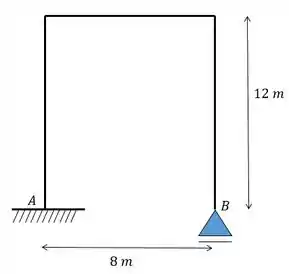
Passo 1
Fala galerinha! Vamos entender o que acontece nesse problemitcho aqui. Primeiro nós tínhamos esse pórtico sem nenhum carga e aí alguém foi lá e rebaixou o ponto em , com isso houve uma deformação no nosso pórtico que gerou diversas cargas!
O problema pede para calcularmos as reações nos apoios devido as esses cargas. A primeira coisa que vamos fazer é transformar a estrutura numa estrutura isostática e depois vamos aplicar uma carga unitária para descobrir a deformação. Com isso vamos poder descobrir o hiperestático e finalmente as reações! Então partiu!
Passo 2
Transformando a estrutura numa estrutura isostática vamos ter:
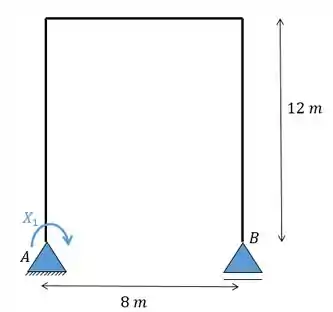
Agora vamos calcular a deformação devida ao recalque utilizando uma carga unitária no lugar de . Lembre-se que vamos dividir em dois sistemas o sistema 0 é o sistema referente ao recalque e o sistema 1 é o sistema referente à .
Passo 3
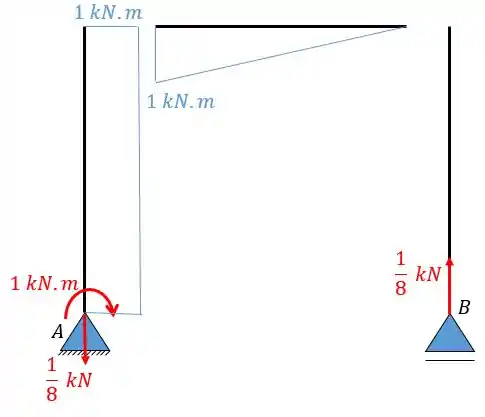
Aplicando a carga unitária vamos ter:
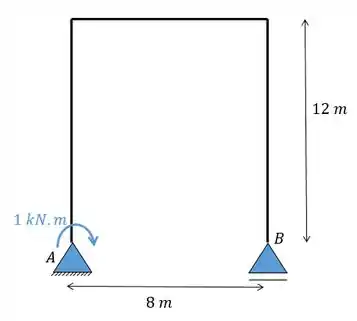
E para calcular a deformação de recalque a gente utiliza nossa formulinha para deformações de recalque:
Para resolver isso vamos fazer dois diagramas, um das forças de reação e outro do recalque:
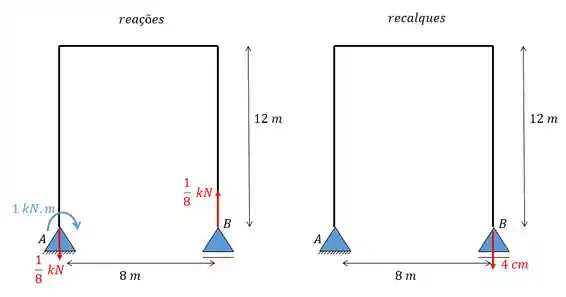
Passo 4
E então vamos relacionar as reações com seus respectivos recalques formando pares. Perceba que o recalque de forma um par com a força de em (pois ambos atuam no mesmo ponto e na mesma direção).
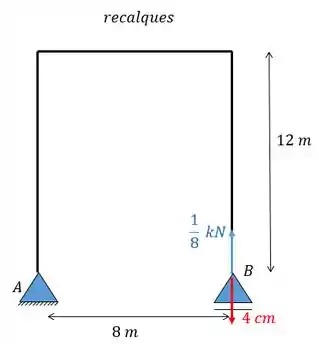
Como não há recalque em podemos olhar só para por enquanto.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,

e sempre que for no sentido contrário, será negativa.

Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
Sabe quem é essa deformação? É exatamente o nosso , então podemos escrever ele como.
Passo 5
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
E para determinar faremos
Como , teremos que
E assim teremos que o nosso sistema será:
Substituindo teremos que
Passo 6
Vamos agora determinar as reações de apoio com as nossas relaçãozinhas
- Reação vertical no apoio esquerdo
- Reação vertical no apoio direito
- Reação vertical no apoio esquerdo
- Reação vertical no apoio direito
- Reação de momento
Resposta
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Determine as reações de apoio do pórtico abaixo, sabendo que o apoio sofre um recalque de para a esquerda e o apoio sofre um recalque de para a direita.
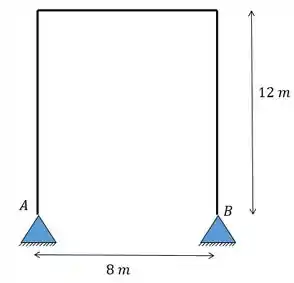
Passo 1
Fala galerinha! Vamos entender o que acontece nesse problemitcho aqui. Primeiro nós tínhamos esse pórtico sem nenhum carga e aí houve uma mudança na configuração dele, com isso houve uma deformação no nosso pórtico que gerou diversas cargas!
O problema pede para calcularmos as reações nos apoios devido as esses cargas. A primeira coisa que vamos fazer é transformar a estrutura numa estrutura isostática e depois vamos aplicar uma carga unitária para descobrir a deformação. Com isso vamos poder descobrir o hiperestático e finalmente as reações! Então partiu!
Passo 2
Transformando a estrutura numa estrutura isostática vamos ter:
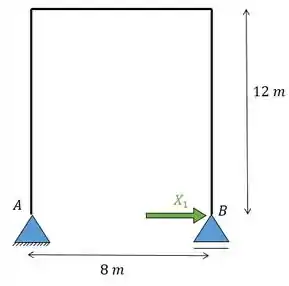
Agora vamos calcular a deformação devida ao recalque utilizando uma carga unitária no lugar de . Lembre-se que vamos dividir em dois sistemas o sistema 0 é o sistema referente ao recalque e o sistema 1 é o sistema referente à .
Passo 3
Aplicando a carga unitária vamos ter:
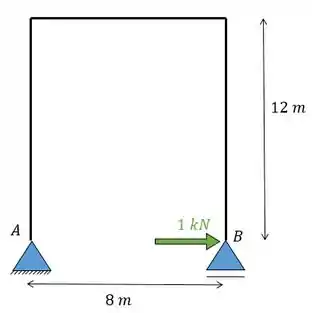
E para calcular a deformação de recalque a gente utiliza nossa formulinha para deformações de recalque:
Para resolver isso vamos fazer dois diagramas, um das forças de reação e outro do recalque:
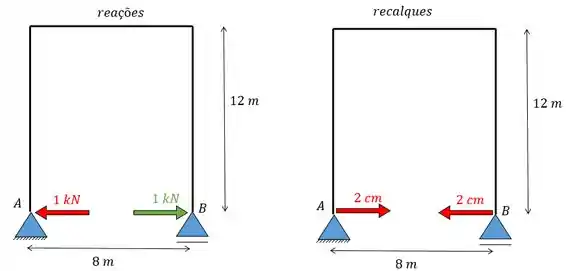
Passo 4
E então vamos relacionar as reações com seus respectivos recalques formando pares.
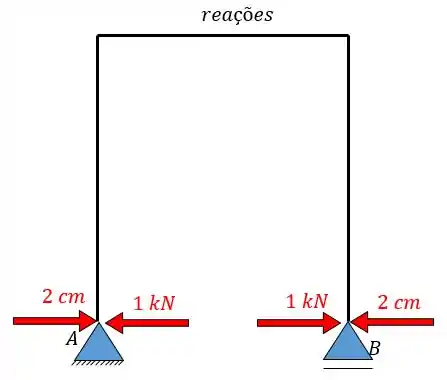
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,

e sempre que for no sentido contrário, será negativa.

Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
Sabe quem é essa deformação? É exatamente o nosso , então podemos escrever ele como.
Passo 5
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
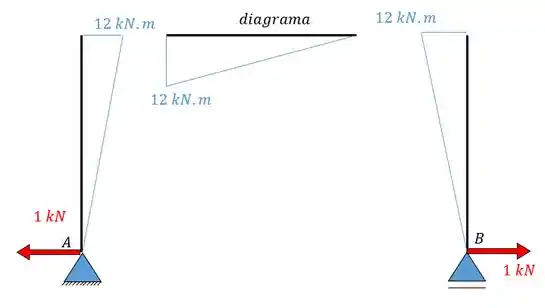
E para determinar faremos
Como , teremos que
E assim teremos que o nosso sistema será:
Substituindo teremos que
Passo 6
Vamos agora determinar as reações de apoio com as nossas relaçãozinhas
- Reação horizontal no apoio esquerdo
- Reação horizontal no apoio direito
- Reação horizontal no apoio esquerdo
- Reação horizontal no apoio direito
- Reação de momento
Resposta
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Origem do Exercício
Determine as reações de apoio do pórtico abaixo, sabendo que o mesmo sofre um recalque vertical para baixo de 2cm no apoio A, e no mesmo apoio sofre um deslocamento de 4cm para direita. E no apoio B, ainda sofre um recalque de 1 cm pra cima.
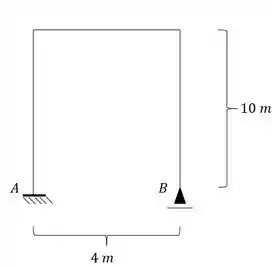
Passo 1
Sabemos que a primeira coisa que devemos fazer é determinar o número de hiperestáticos.
- Hiperestáticos totais pelo macete
- Sabemos que temos 1 apoio do terceiro gênero e um apoio do primeiro gênero, totalizando 4 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
Ou seja, nossa estrutura possui um grau de hiperestaticidade, que se eu conseguir tirar da nossa estrutura, transforma a nossa estrutura em isostática.
Quebrando um vinculo teremos a seguinte nova estrutura.
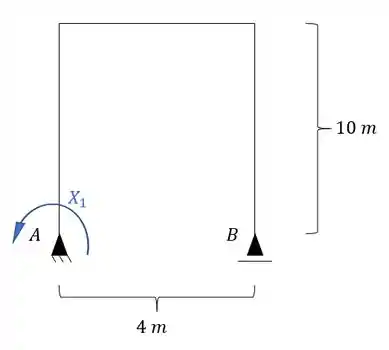
E até aqui a gente sabe resolver de boas, o que aparece de novo é o seguinte.
Pra determinar a deformação no sistema zero, que nesse caso é um recalque de apoio, precisamos obrigatoriamente colocar uma carga unitária no mesmo lugar, na mesma direção e no mesmo sentido do hiperestático, porém iremos calcular a deformação de maneira DIFERENTE do que fazemos com o hiperestático.
Apesar da carga estar na mesma posição e sentido do hiperestático, para o hiperestático iremos calcular o diagrama de momentos, porém para o sistema zero iremos calcular as deformações de recalque. Parece meio embolado, mas é bem tranquilo, me segue aqui.
Passo 2
Como eu disse, no sistema zero colocamos uma carga unitária na mesma posição, direção e sentido do hiperestático, com isso teremos.
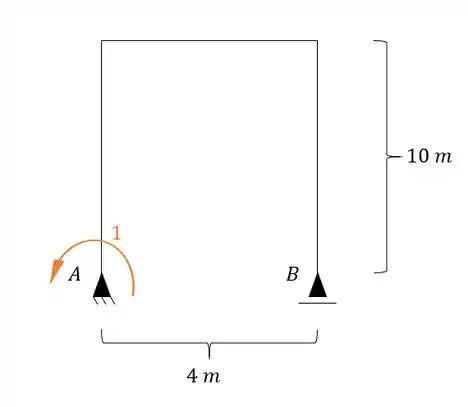
Para esse sistema como definimos a deformação quando estamos vendo o recalque? Não seria exatamente calculando as reações de apoio, e usando a nossa formulazinha?
Determinando as reações de apoio desse sistema teremos que:
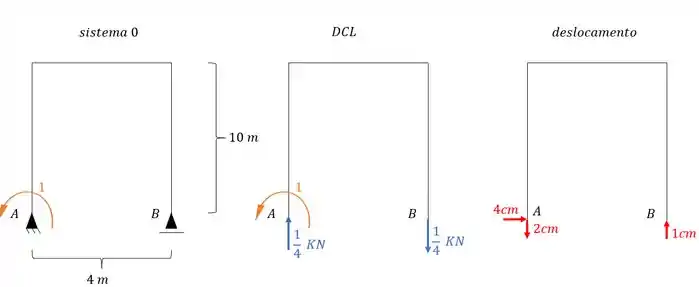
E como eu disse, precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
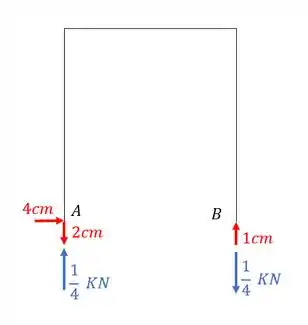
Como o 4cm não tem par, só iremos ter dois termos.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,

e sempre que for no sentido contrário, será negativa.

Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
Sabe quem é essa deformação? É exatamente o nosso , então podemos escrever ele como.
Passo 3
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
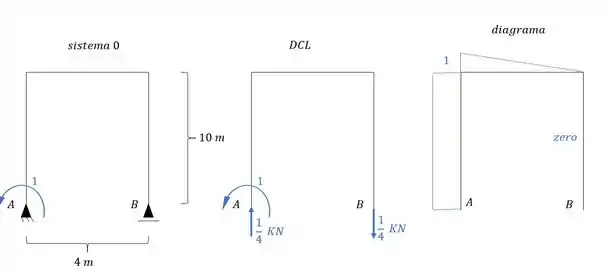
E para determinar faremos
Como , teremos que
E assim teremos que o nosso sistema será:
Substituindo teremos que
Vamos agora determinar as reações de apoio com as nossas relaçãozinhas
- Reação vertical no apoio esquerdo
- Reação vertical no apoio direito
- Reação vertical no apoio esquerdo
- Reação vertical no apoio direito
- Reação de momento
Resposta
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Origem do Exercício
Determine as reações de apoio do pórtico abaixo, sabendo que o mesmo sofre um recalque vertical para baixo de 5cm no apoio A. E no apoio B, ainda sofre um recalque de 10 cm pra cima e 3 cm para direita.
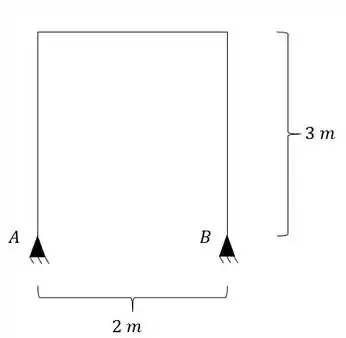
Passo 1
Sabemos que a primeira coisa que devemos fazer é determinar o número de hiperestáticos.
- Hiperestáticos totais pelo macete
- Sabemos que temos 2 apoios do segundo gênero, totalizando 4 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
Ou seja, nossa estrutura possui um grau de hiperestaticidade, que se eu conseguir tirar da nossa estrutura, transforma a nossa estrutura em isostática.
Quebrando um vinculo teremos a seguinte nova estrutura.
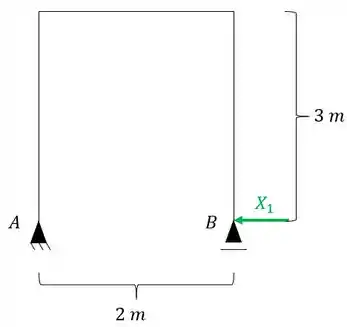
E até aqui a gente sabe resolver de boas, o que aparece de novo é o seguinte.
Pra determinar a deformação no sistema zero, que nesse caso é um recalque de apoio, precisamos obrigatoriamente colocar uma carga unitária no mesmo lugar, na mesma direção e no mesmo sentido do hiperestático, porém iremos calcular a deformação de maneira DIFERENTE do que fazemos com o hiperestático.
Apesar da carga estar na mesma posição e sentido do hiperestático, para o hiperestático iremos calcular o diagrama de momentos, porém para o sistema zero iremos calcular as deformações de recalque. Parece meio embolado, mas é bem tranquilo, me segue aqui.
Passo 2
Como eu disse, no sistema zero colocamos uma carga unitária na mesma posição, direção e sentido do hiperestático, com isso teremos.
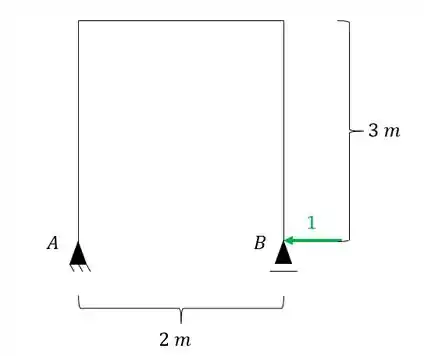
Para esse sistema como definimos a deformação quando estamos vendo o recalque? Não seria exatamente calculando as reações de apoio, e usando a nossa formulazinha?
Determinando as reações de apoio desse sistema teremos que:
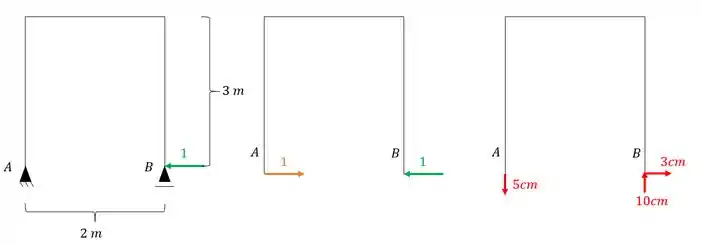
E como eu disse, precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
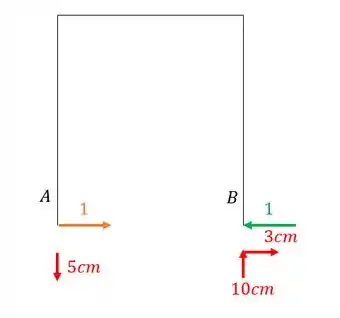
Como o 4cm não tem par, só iremos ter dois termos.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,

e sempre que for no sentido contrário, será negativa.

Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
Sabe quem é essa deformação? É exatamente o nosso , então podemos escrever ele como.
Passo 3
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
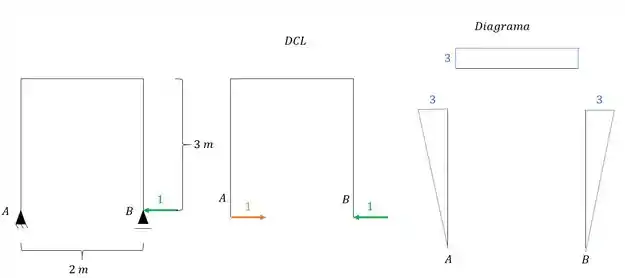
E para determinar faremos
Como , teremos que
E assim teremos que o nosso sistema será:
Substituindo teremos que
Como só tivemos reações horizontais sabemos que as reações serão dadas por:

Resposta
Reações horizontais de apoio
