
- Determine a estimativa da linha de regressão do número de erros em função do número de horas sem dormir.
- Construa uma tabela ANOVA
- Ache o R² e interprete
Passo 1
No exercício precisamos encontrar, a reta de regressão, tabela ANOVA, e interpretar alguns resultados como significância da regressão por exemplo:
Passo 2
Para resolvermos a letra A precisamos achar os estimadores dos parâmetros, se você tem dificuldade com isso de uma relembrada na parte de mínimos quadrados. A reta é:
Passo 3
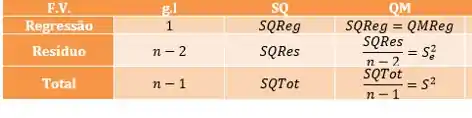
Agora para resolvermos a letra B precisamos completar os dados que faltam da tabela (no caso todos)
Passo 4
Para calcular a letra d, vamos calcular o R², que tem a fórmula
Um pouco acima de 50%, porém não é tão bom assim
Resposta
Ei, a resposta está no passo a passo :)