Um estudo sobre duração de certas operações está investigando o tempo requerido (em segundos) para acondicionar objetos e o volume (em ) que eles ocupam. Uma amostra foi observada e obtiveram-se os seguintes resultados:

a) Faça o diagrama de dispersão dos dados.
b) Estime a reta de regressão do tempo de operação em função do volume.
c) Construa a tabela ANOVA para o modelo.
d) Qual o valor de ? É pequeno quando comparado a
e) Você acha que conhecer o volume do pacote ajuda a prever o tempo de empacotamento?
Passo 1
Neste exercício precisaremos ter muita atenção pois aplicaremos quase tudo que vimos, montar o gráfico dos pares de dados, estimar a reta de regressão e montar a tabela anova!
Passo 2
Para montar o gráfico pegamos os pares de dados e plotamos eles, mais ou menos assim
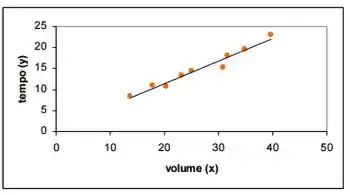
Passo 3
Agora para a letra b precisamos estimar os valores para α e β, só aplicar a fórmula de minímos quadrados, caso você esteja com alguma dificuldade nessa parte recomendo que revise a teoria 1 deste tópico, mas atente-se em que você escolhe como x e y.
A reta será
Passo 4
Na letra C é que teremos trabalho, para montarmos a tabela ANOVA vamos precisa lembrar algumas coisas, tais como
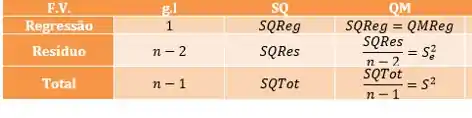
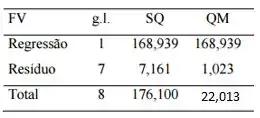
Passo 5
Para resolver esta letra basta checarmos a tabela anova pra ver que e . E assim é possível perceber que é realmente pequeno comparando um ao outro.
Passo 6
Após todas as análises que fizemos, podemos sim concluir que conhecer o volume do pacote ajuda a prever o tempo de conhecimento, isto é, a regressão é significativa.
Resposta
Ei, a resposta está no passo a passo :)