Otimização
Teoria
Hoje vamos ajudar o Ruan, que depois de muitos anos dando aula no Responde Aí, virou fazendeiro. Ruan comprou arame suficiente pra de cerca pra fechar um espaço retangular da sua fazenda onde vai criar vacas. Como sua fazenda é bem grande, pra dar bastante espaço pros bichos, ele quer cercar a maior área possível usando todo o arame que comprou. Quais são as dimensões ideais do cercado?
Bom, essa história pode até te parecer meio estranha, mas esse é um problema clássico de otimização, e hoje vamos aprender como resolver problemas como esse usando derivadas!
Identificando problemas de otimização
Antes de começarmos, é importante você saber do que estamos falando, então deixa eu explicar o que é otimização: são problemas como esse, onde queremos encontrar os valores que geram o máximo ou mínimo de uma variável específica. No caso da fazenda, queremos encontrar as dimensões do espaço retangular que geram a maior área cercada possível.
Problemas assim podem aparecer nos contextos mais diversos, quando queremos minimizar ou maximizar áreas, volumes, custos, distâncias, etc. Por causa dessa diversidade toda, é bem importante saber resolver esses problemas.
Então bora lá!
Resolvendo problemas de otimização
Vou mostrar o passo a passo pra resolver problemas desse tipo, mas é importante ter algo em mente: como esses problemas podem surgir em contextos muito diferentes, não existe uma fórmula fechadinha que sirva pra resolver todos eles, então é importante que você entenda o caminho que vamos percorrer pra chegar na solução, pra depois conseguir aplicar usando as condições específicas do problema que você tiver.
Passo 1. Identificar as variáveis e funções
O primeiro passo consiste em organizar todas as informações que temos, já que, geralmente, esses problemas vêm como um textinho e as coisas estão todas perdidas lá no meio.
Tem dois elementos principais que precisamos identificar aqui: as variáveis que vamos trabalhar e a função que será otimizada.
Aqui, as variáveis que estamos trabalhando são as dimensões do cercado retangular, que vou chamar de e . Nessa etapa, fazer um desenho ajuda muito!
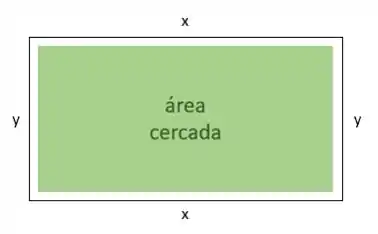
Queremos otimizar a área, ou seja, encontrar os valores de e que correspondam a maior área possível. Como precisamos escrever isso como uma função, vamos usar a relação geométrica pra área de um retângulo:
Pra fechar, o problema nos deu mais uma informação importante: Ruan tem material pra fazer de cerca. Isso é importante porque serve pra limitar nossas contas, mas pra isso, precisamos escrever a informação usando as variáveis que criamos. Aqui, esse valor vai funcionar como perímetro, a soma total dos lados do nosso cercado retangular:
Agora que organizamos todas as informações, bora pro próximo passo!
Passo 2. Reescrever a função que será otimizada com apenas uma variável
Lembra que lá atrás eu disse que vamos resolver o problema usando derivadas? Bom, pra derivar aqui, vamos escrever a função só com uma variável.
Lembrando que nossa função é:
Então precisamos tirar o ou o , pra isso vamos usar a informação dos de cerca, que pode ser reescrita como:
Isolamos o pra substituir lá na nossa função, que agora fica só em termos de :
Obs.: Nem sempre vai ser necessário fazer esse passo, já que em alguns problemas a função dada já vai estar com uma variável só. Mas fica atento, porque ele vai ser muito importante quando tivermos mais de uma variável!
Passo 3. Encontrar máximos ou mínimos da função
Chegamos no passo onde as respostas começam a surgir! Agora que temos uma função prontinha, vamos encontrar os máximos ou mínimos, de acordo com o que o problema pedir.
Primeiro, vamos derivar a função:
Agora, vamos encontrar os pontos críticos, igualando a derivada a zero e resolvendo a equação:
Então, precisamos calcular a derivada segunda para descobrir se o ponto encontrado é de máximo ou de mínimo:
Lembrando que os critérios pro teste da segunda derivada são:
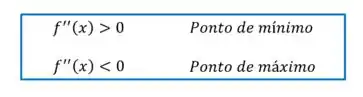
Como é sempre negativo, o ponto crítico que encontramos é um ponto de máximo, exatamente como queríamos!
Passo 4. Testar fronteiras
Em alguns casos, o máximo ou mínimo da função pode estar nas fronteiras, ou seja, nos extremos das variáveis que podem ser , , ou outros valores dependendo do problema, e o processo que fizemos derivando a função não vai mostrar isso. Então, é importante testar esses valores.
Aqui no nosso problema, vamos lembrar o que o representa:
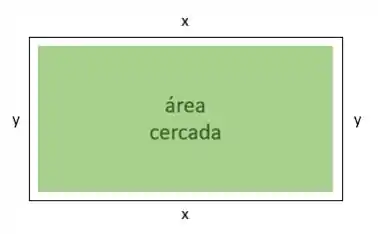
Primeiro, vamos pensar em qual é o menor valor possível de . Como não faz sentido falar de comprimento negativo, o menor vai ser um valor muuuito pequeno e positivo próximo de zero. Vamos representar isso com um limite da função de área com :
Já a outra fronteira representa o maior possível, considerando que temos só de cerca e que qualquer valor de que escolhemos vai estar representando dois lados do retângulo, o maior possível seria um valor muuuito próximo a . Novamente, vamos representar isso com um limite, onde :
Vimos então que em ambas fronteiras, com muito pequeno ou muito grande, a área cercada tende a ser zero, então nosso valor máximo vai ser o que encontramos no passo anterior, .
Passo 5. Usar o ponto de máximo ou mínimo encontrado para encontrar as outras variáveis correspondentes
Como ficamos com o , é esse valor que vamos usar para encontrar os valores correspondentes das outras variáveis.
Podemos usar a relação com isolado para encontrar o outro lado do retângulo:
Com e , podemos calcular a área máxima encontrada:
E está resolvido o problema! Com essas dimensões, temos a maior área cercada possível pra criação das vacas.

Pra encerrar, vale lembrar que os problemas de otimização podem surgir com caras bem diferentes. Então sempre que falarem de máximos ou mínimos, fica ligadinho que pode ser um desses problemas.
E pra ficar craque na resolução, só treinando bastante mesmo, então bora pros exercícios!
Exercícios Resolvidos
Exercício Resolvido #1
UNIP – Cálculo 1 - Apostila
O produto de dois números inteiros e positivos resulta em 100. Quais são esses números, sabendo que sua soma resulta no menor valor possível?
Passo 1
Olááá! Tudo certinho?
Do enunciado, vemos que nosso objetivo aqui é encontrar dois números desconhecidos que geram o menor resultado possível quando somados.
“O menor resultado possível” é a dica que o problema nos dá pra sacar que se trata de um problema de otimização!
Nosso primeiro passo nesses problemas sempre é organizar as informações que o enunciado tá passando! Então bora lá!
Vamos chamar os dois números desconhecidos de e , então, se o produto entre os dois resulta em , podemos dizer que:
Como queremos que a soma seja o menor possível, é dela que surge a função que vamos otimizar. Escrevendo uma função pra soma, temos:
Passo 2
Como resolvemos os problemas de otimização usando derivadas, queremos que nossa função dependa de só uma variável, pra isso, vamos reescrever a expressão do produto de um jeito que possamos substituir na função soma e tirar uma das variáveis.
Olha:
Que substituindo na função, resulta em:
Agora nossa função tá prontinha pra ser derivada!
Passo 3
Podemos reescrever a função usando a propriedade onde subimos ou descemos a potência na fração trocando o sinal do expoente:
Desse jeito, fica mais fácil usar a regra do peteleco pra derivar:
Mais uma vez com a propriedade das potências, temos:
Passo 4
Para encontrar os pontos críticos da função, que são nossos candidatos a mínimo da função, vamos igualar a derivada a zero e resolver a equação:
Temos então dois candidatos: e
Passo 5
Como o enunciado especifica que os números são inteiros e positivos, podemos descartar o .
Vamos testar pra ter certeza que de fato temos um ponto de mínimo. Pra isso, precisamos da segunda derivada da função.
Derivando mais uma vez, temos:
Testando quando , temos:
O critério do teste da segunda derivada é o seguinte:
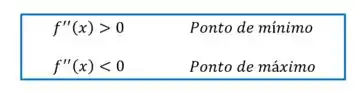
Como encontramos um resultado positivo, é um ponto de mínimo, exatamente como queríamos!
Passo 6
Pra encerrar, precisamos encontrar também o valor de , já que a questão pede os dois números!
Podemos substituir lá na primeira expressão que escrevemos pro produto igual a :
Prontinho!
Resposta
Exercício Resolvido #2
Uma pessoa dispõe de de arame para cercar um terreno retangular. Utilizando o conceito de derivada, determine as dimensões deste terreno para que o mesmo apresente área máxima.
Passo 1
Beleza, a princípio temos um terreno com a seguinte cara:
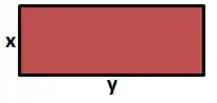
O que o problema quer que a gente descubra, são os valores de e de que fazem com que ele tenha a maior área possível. Então vamos descobrir quem é a função que descreve a área e encontrar os valores de e de que fazem seu valor ser máximo, pra isso usaremos os conceitos de derivada que estamos estudando.
O enunciado nos afirma que o cercado em preto é de . Ou seja, o seu perímetro, que é a soma de todos os lado, é:
Podemos simplificar essa expressão, dividindo tudo por . Isso vai facilitar os nossos cálculos mais à frente.
Agora vamos falar sobre a área desse terreno. Ela é a multiplicação de um lado pelo outro, certo? Então
Mas derivar uma função com duas variáveis não vai rolar por agora, então podemos isolar o lá na expressão do perímetro, ficando com
Agora é só substituir isso na expressão da área:
Prontinho, achamos a função que descreve a área desse terreno.
Passo 2
Para encontrarmos a maior área possível, vamos procurar o valor máximo da função área que a gente acabou de encontrar no passo anterior. Pra isso precisamos fazer a primeira derivada dela e depois igualar a zero. Lembra que pra acharmos os valores de máximos e mínimos nós fazemos a primeira derivada igual a zero? Então...isso que faremos agora.
Mãos a obra!
Achamos a derivada. Agora vamos igualar a zero e encontrar o valor de nesse ponto....
Passo 3
Para ter certeza que o ponto que encontramos é de máximo mesmo, podemos fazer o teste da segunda derivada.
Pra isso, vamos derivar mais uma vez a função área:
O critério do teste diz que:
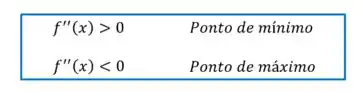
Como a segunda derivada que encontramos é negativa, temos um ponto de máximo!
Passo 4
Agora vamos atrás do valor de .
Como vimos antes
Substituindo :
Ou seja, esse nosso retângulo será na verdade um quadrado com lado , tendo a maior área possível de ser cercada com a quantidade de arame disponível.
Resposta
Exercício Resolvido #3
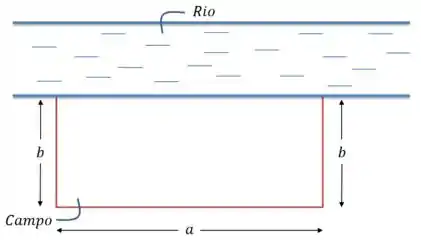
Um fazendeiro tem de cerca e quer cercar um campo retangular que está na margem de um rio reto. Ele não precisa cercar o lado do terremo que ficará a margem do rio. Quais são as dimensões que ele deve usar para obter um campo com a maior área possível, podendo ser cercando com a quantidade de cerca disponível?
(a) por
(b) por
(c) por
(d) por
(e) por
Passo 1
E aí, tudo beleza?
Dá uma olhadinha no desenho aqui pra entender melhor:
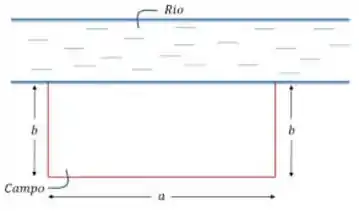
Ali temos o campo, de lados sendo que em um dos lados medindo temos a margem do rio.
Queremos saber quais sãos os valores de , nessas condições, para que o campo tenha área máxima. Vem comigo!
Passo 2
A questão nos disse que o fazendeiro tem de cerca, e a quantidade de cerca de um campo retangular é dado pelo perímetro (soma dos lados) dele.
Nesse caso vamos somar os lados com exceção do lado à margem do rio. Temos:
Como temos de cerca, nosso perímetro deverá ser:
Vamos colocar e função de :
Ok, encontramos uma relação entre os dois lados do campo. Guarda isso por enquanto!
Passo 3
A gente quer encontrar a área máxima, sendo que área do campo é dada por:
Mas, a gente achou ali em cima que:
Bora jogar isso no lugar de de na expressão da área, então?
Fazendo a distributiva:
Encontramos a expressão da área em função de 😊
Passo 4
Como queremos encontrar a maior área possível, vamos maximizar essa função:
Pra achar o ponto máximo dela, vamos encontrar onde a derivada dá zero. Vamos derivar usando a regra do Tombo:
Passo 5
Ótimo! Agora vamos ver onde essa derivada zera:
Show! Achamos o valor de que faz com que a área seja máxima!
Passo 6
Importante conferir se o ponto que encontramos é mesmo um ponto de máximo, pra isso vamos derivar a função área mais uma vez:
O teste da segunda derivada nos diz o seguinte:
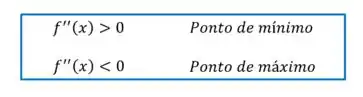
Como encontramos uma segunda derivada negativa, o ponto é um ponto de máximo!
Passo 7
Pra achar o valor da dimensão é mais fácil, porque a gente já viu que:
E como , temos:
Show de bola!
Então para que tenha área máxima, nessas condições, o campo deve medir por 😉
Resposta
Exercício Resolvido #4
UERJ - Cálculo 1 - Lista Derivadas – 6
Um campo retangular à margem de um rio deve ser cercado com exceção do lado ao longo do rio. Se o custo do material for de no lado paralelo ao rio e de nos dois extremos, ache o campo de maior área que possa ser cercado com de materiais.
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Bom, comecei desenhando esse caso aí:
A área do retângulo, que é o formato do campo, vai ser dada por:
Passo 2
Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
Temos como limitante aquele preço de . Bom, se custa a cerca do lado paralelo e a dos outros dois, posso criar um custo, estando e em metros, dado por essa equação:
Repara que são dois lados de comprimento e um lado . Como ele diz que esse custo é fixo em , ficamos assim:
Passo 3
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Vamos isolar o na nossa expressão do custo:
Juntando a última equação à da área, temos:
Passo 4
Agora derivamos essa função e achamos os pontos críticos.
Se eu procuro o ponto crítico da área, ou seja, a maior possível, devo derivar essa função:
Então, igualamos a zero para encontrar os pontos críticos, que são nossos candidatos a máximo:
Passo 5
Analisamos os pontos críticos encontrados para garantir que sejam máximo ou mínimo.
Como a derivada é fácil de calcular, é melhor derivar de novo e aplicar o teste da segunda derivada.
Como a segunda derivada é negativa, esse é um ponto de máximo.
Obs.: Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor). Mas como não há outros pontos críticos a calcular, então, próximo passo!
Passo 6
Pegamos o ponto crítico obtido e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
Olhando para função área:
Vemos que o menor valor para é zero, uma vez que é uma medida. O maior é .
Para zero, a área é zero e inútil pro que queremos.
Para :
O que também não é aplicável. Dessa maneira é um ponto de máximo global, onde:
Eu sei que ficou feio, mas esse é nosso resultado.
Resposta
Exercício Resolvido #5
Se de material estiverem disponíveis para fazer uma caixa com uma base quadrada e sem tampa, encontre o maior volume possível da caixa.
(a)
(b)
(c)
(d)
(e) Nenhume das alternativas
Passo 1
E aí, tudo bem?
Já que a base é quadrada, queremos uma caixa mais ou menos assim:
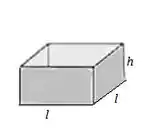
O enunciado também nos deu que estão disponíveis de material para fazer essa caixa.
A nossa restrição então é que a área total dela é 1200.
Vamos colocar em linguagem matemática...
Passo 2
A área total dessa caixa é dada pela soma das áreas de cada pedacinho.
Temos a base, que é:
E temos 4 laterais retangulares, medindo por , ou seja:
A área total vai ser a soma da área da base mais as áreas laterais. Então ela será dada por:
E como a área total é 1200, temos:
Ok, segura isso por enquanto!
Passo 3
Vamos lá, a gente quer encontrar o maior volume possível pra caixa, dentro da condição que a gente viu ali em cima.
O volume da caixa (que é um paralelepípedo) é calculado assim:
Vamos colocar isso em função de uma variável só usando a condição que achamos ali em cima.
Passo 4
A gente pode isolar o nessa expressão aqui pra deixar em função de :
Vamos substituir na fórmula do volume agora:
Simplificando o :
Passo 5
Beleza, agora que temos a função a ser maximizada em termos de uma variável só. Podemos partir para a derivada:
Agora, vamos igualar a zero para encontrar os pontos críticos:
Como estamos falando de medidas, ficamos só com o valor positivo .
Passo 6
Ok, agora é só acharmos o valor de que acompanha esse e depois calcular o volume!
E então o volume máximo possível é:
Alternativa (a) 😊
Resposta
Exercício Resolvido #6
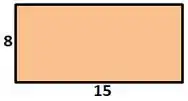
Um pedaço de papel retangular é usado para construir uma caixa sem tampa, pra isso corta-se quadrados iguais de cada canto do papel. O papel retangular possui 8 centímetros de largura por 15 centímetros de comprimento. Determine o volume máximo para tal caixa.
- Aproximadamente 90,74;
- Exatamente 60;
- Aproximadamente 80;
- Aproximadamente 50;
- Nenhuma das respostas anteriores.
Passo 1
Vamos pensar no nosso retângulo, o enunciado nos mostra que ele é assim ó
 O enunciado nos disse que ele vai recortar quadrados nos quatro cantos, então teremos o seguinte:
O enunciado nos disse que ele vai recortar quadrados nos quatro cantos, então teremos o seguinte:
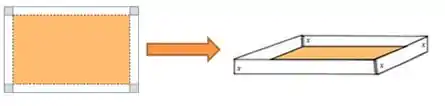
Vamos chamar os lados dos quadrados que serão cortados de , com isso, as medidas na folha são:
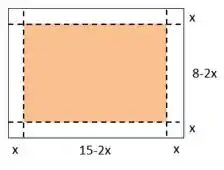
O volume dessa caixa, será:
Se você for observar bonitinho aquele desenho, vai ver que a altura vale , certo? A largura dela vale e o comprimento vale , então agora é substituir isso aí na nossa fórmula do volume.
Resolvendo as multiplicações, teremos:
Passo 2
Como ele pediu o maior volume possível da caixa, teremos que achar o valor máximo da função volume.
Para encontrarmos os pontos de máximo e mínimo, vamos fazer a primeira derivada e igualar ela a zero! Grava isso...máximo e mínimo, primeira derivada igual a zero
Derivando, teremos:
Observa que a derivada da soma é igual a soma das derivadas, certo? Então
Observa que deixei todas as constantes de fora da derivada.
Agora é só derivar tudo aí. Vamos lembrar a derivada de polinômio?
Então
Agora vamos igualar isso a zero e encontrar as raízes
Resolvemos essa equação do segundo grau pra ver onde que ela vale zero. Primeiro vem nosso delta
Detalhe, no nosso caso temos
Vamos jogar nas fórmulas, então. Primeiro calculando o delta
Ou seja, temos duas raízes:
Beleza, agora precisamos ver qual das duas nos dá o maior e o menor volume possível...
Vamos substituir esses valores na expressão que encontramos para o volume, essa aqui ó:
Primeiro o
Fazendo o
Esse obviamente, vamos descartar porque não faz sentido termos um volume negativo!
Sendo assim, o volume é proximo de ! Letra A!
Resposta
Exercício Resolvido #7
UniCesumar - Cálculo 1 – Avaliação Online
Uma folha de papelão com de área será utilizada para confeccionar um cartaz. As margens livres do topo e da base do cartaz devem ter e as laterais, . Determine as dimensões da folha de modo que a área útil seja máxima.
Passo 1
Como queremos que a área útil seja máxima, temos um problema de otimização.
Vamos começar organizando os dados e montando um esquema!
É bem importante nessa questão entender bem a diferença entre a área total, que é de , e a área útil, que é o que queremos otimizar. Dá uma olhada:
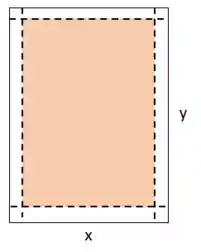
Chamei as medidas da folha de e , já que não as conhecemos.
A área total, que inclui as margens, pode ser calculada da seguinte forma:
Se considerarmos só a parte laranja, temos a área útil, que é essa parte do meio que desconsidera as margens e é calculada por:
Subtraímos duas vezes a medida da margem lateral do e duas vezes a medida da margem da base do . Essa função que precisamos otimizar!
Obs.: Pra colocar as medidas das margens na fórmula eu converti de cm para m dividindo por 100.
Passo 2
Agora precisamos reescrever a função pra derivar, pra isso, podemos usar a relação da área total:
Substituindo na função de área útil:
Vamos fazer as multiplicações:
Enfim, nossa função tá prontinha pra ser derivada!
Passo 3
Pra derivar, vamos usar a regra do peteleco, então fica mais fácil ver a função como:
Derivando, temos:
Passo 4
Para encontrar os pontos críticos, que são nossos candidatos a máximo da função, precisamos igualar a derivada a zero e resolver a equação:
Vamos multiplicar essa fração para encontrar valores inteiros e mais fáceis de seguirmos com as contas:
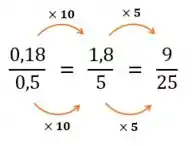
Temos, então:
Como estamos falando de medidas, não faz sentido ter valores negativos, então já podemos desconsiderar .
Temos então a área útil máxima quando !
Passo 5
Pra encerrar, vamos determinar o correspondente. Pra isso, vamos usar a relação da área total:
Prontinho!
Resposta
Exercício Resolvido #8
UniCesumar - Cálculo 1 – Avaliação Online
Determine a área máxima possível de um triângulo retângulo de hipotenusa .
Passo 1
Como queremos a área máxima possível, temos um problema de otimização!
Nosso primeiro passo sempre é organizar as informações que temos do enunciado e, sempre que possível, fazer um desenho.
Queremos a área máxima de um triângulo retângulo (onde um dos ângulos é ) com hipotenusa de . Podemos chamar os dois catetos desconhecidos de e , com isso temos:
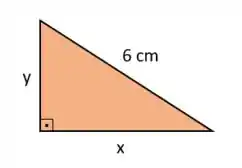
Como queremos otimizar a área, vamos escrever uma função pra ela usando a fórmula de área dos triângulos:
Passo 2
Os problemas de otimização são resolvidos com derivada, pra isso precisamos reescrever a função área como uma função de uma só variável.
Como temos um triângulo retângulo, podemos usar o teorema de Pitágoras para relacionar os valores desconhecidos e :
Vamos substituir essa relação lá na função área que escrevemos:
Passo 3
Com a função escrita só em termos de já podemos derivar, mas pra facilitar um pouco, vamos reorganizar um pouco as coisas...
Primeiro, colocando o pra dentro da raiz, que pra isso fica ao quadrado:
Vamos lembrar também que toda raiz pode ser reescrita como , temos então:
Bora derivar!
Temos uma função dentro de outra, então precisamos usar a regra da cadeia: vamos derivar a função de fora, que no caso é o expoente , e multiplicar pela derivada da função de dentro :
Já aplicamos a regra do tombo fora, agora aplicamos dentro:
Podemos descer o segundo termo trocando o sinal do expoente:
Por fim, vamos reescrever a raiz:

Eu sei, ficou uma coisa horrível... Mas eu te prometo que daqui pra frente vai tudo ficar mais simples!
Passo 4
Para encontrar os pontos críticos, nossos candidatos a máximo da função, precisamos igualar a derivada a zero.
Trazendo nosso monstrinho, temos:
O some quando passamos pro outro lado, que vai continuar sendo zero
Independente do que temos no denominador, uma fração vai ser zero quando seu numerador for zero, então pra gente só vai importar:
Viu? Muito mais simples!

Dividindo a expressão por , temos:
Prontinho, achamos o valor de um dos lados do triângulo que gera a área máxima!
Passo 5
Agora, vamos substituir na nossa relação de Pitágoras para encontrar o :
Passo 6
Finalmente, pra encontrar a área máxima substituímos os dois lados na fórmula da área:
Resolvido!
Resposta
Exercício Resolvido #9
UNIP – Cálculo 1 - Apostila
Deseja-se fabricar um recipiente cilíndrico com tampa com capacidade volumétrica de . O material destinado à lateral do recipiente custa o enquanto o material destinado ao fundo custa o . Determine a altura e o raio do recipiente de modo que o custo de fabricação seja minimizado.
Passo 1
Bom, vamos começar desenhando um recipiente cilíndrico com suas dimensões principais o raio e a altura :
O volume do cilindro é dado pela fórmula:
Além disso, temos os custos: a parte lateral, mais escura no desenho, custa , podemos calcular essa área da seguinte forma
Enquanto a tampa e a base custam e tem sua área dada por:
Passo 2
Como queremos minimizar o custo da fabricação do recipiente, precisamos de uma função que represente esse custo. Vamos encontrar essa função pela soma das áreas multiplicadas pelos seus custos respectivos:
Obs.: Lembrando que temos base e tampa, por isso essa área entra multiplicada por 2
Simplificando a função, temos:
Passo 3
Vamos precisar da função com apenas uma variável para derivar, pra isso, vamos usar a relação do volume:
Podemos isolar o :
Agora, substituímos na função custo:
Passo 4
Agora, para encontrar os pontos críticos, vamos derivar a função custo usando a regra do peteleco:
E então, igualar a derivada a zero:
Passo 5
Finalmente, vamos calcular a altura usando a relação do volume lá do Passo 3: